Next: Yet another way to Up: , , and the Previous: , , and the
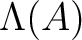 for arbitrary commutative ring
for arbitrary commutative ring 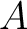
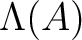 for
for 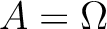 , a field of characteristic 0.
Now we want to define the structure for arbitrary commutative ring
, a field of characteristic 0.
Now we want to define the structure for arbitrary commutative ring  .
Note that addition is already known:
.
Note that addition is already known:
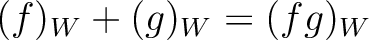
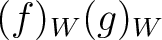 .
Before doing that, we consider “universal” power serieses:
.
Before doing that, we consider “universal” power serieses:
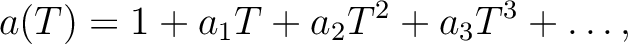 | ||
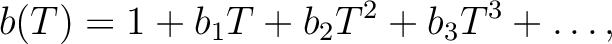 |
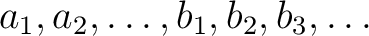 be all independent variables.
We need a fairly large field
be all independent variables.
We need a fairly large field  , namely,
, namely,

 .
We find:
.
We find:
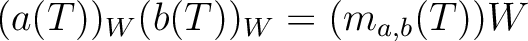
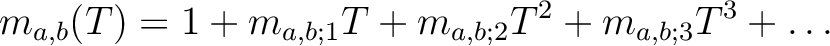
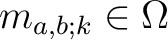 .
.
We also see:
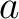 ,
, 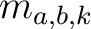 only depend on
only depend on
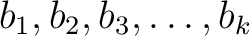 .
(In other words, it is an element of
.
(In other words, it is an element of
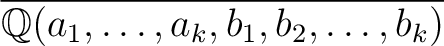 .
.
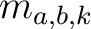 actually lie in
actually lie in
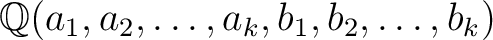 .
.
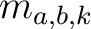 is integral over
the polynomial ring
is integral over
the polynomial ring
![$\mathbb{Z}[a_1,a_2,\dots,a_k,b_1,b_2,\dots, b_k]$](img23.png) . It is thus itself belongs to
the ring
. It is thus itself belongs to
the ring
![$\mathbb{Z}[a_1,a_2,\dots,a_k,b_1,b_2,\dots, b_k]$](img23.png) .
.
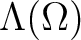 obeys each of the axioms of ring,
such as
obeys each of the axioms of ring,
such as
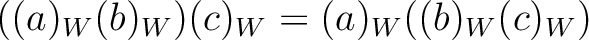
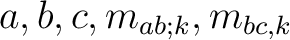 .
Such identities in term guarantees that for any ring
.
Such identities in term guarantees that for any ring 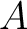 ,
,
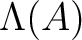 satisfy such axiom.
satisfy such axiom.
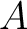 ,
,
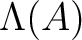 carries the
structure of a ring.
carries the
structure of a ring.