Next: About this document ...
 《ベズーの等式》
《ベズーの等式》
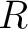 の元
の元 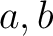 に対して、次は同値である。
に対して、次は同値である。
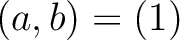
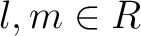 が存在して、
が存在して、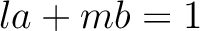 が成り立つ。
が成り立つ。
ユークリッド環については、最大公約数が 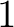 であるような
であるような 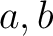 に対して、
上の命題のような
に対して、
上の命題のような 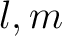 は互除法により求まるのであった。
は互除法により求まるのであった。
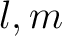 は色々な意味で大事であるので、今回はその解説をしたい。
例としてつぎのような定理、命題を考える。(いくつかは既出である。)
は色々な意味で大事であるので、今回はその解説をしたい。
例としてつぎのような定理、命題を考える。(いくつかは既出である。)
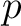 が素数であれば、
が素数であれば、
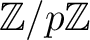 は体である。
は体である。
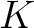 上の 既約多項式
上の 既約多項式 ![$p\in K[X]$](img12.png) にたいして、
にたいして、![$K[X]/p(X)$](img13.png) は体である。
は体である。
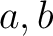 は互いに素な正の整数とする。
群
は互いに素な正の整数とする。
群 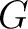 の元
の元 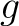 が
が 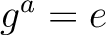 ,
, 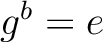 (
(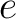 は
は 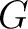 の単位元)を満足するならば、
の単位元)を満足するならば、
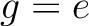 である。
である。