Next: About this document ...

単項イデアル環であるような整域を単項イデアル整域 (principal ideal domain, 略してPID)とよぶ。
 において、
において、 の元
の元  をとる。
をとる。
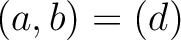 を満たす
を満たす  は
は  の最大公約元である。
の最大公約元である。
 の元
の元  が
が
 かつ
かつ  を満たすならば、
を満たすならば、  .
.
 は可換環であるとする。
は可換環であるとする。 の元
の元  が既約であるとは、
が既約であるとは、  が 0 でも可逆元でもなく、なおかつ
が 0 でも可逆元でもなく、なおかつ
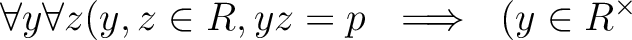 または
または 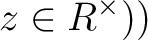
 においては、既約元は素元である。
においては、既約元は素元である。
 が素元分解環であるとは、
が素元分解環であるとは、 の
任意の元
の
任意の元  について、次のいずれかが成り立つときに言う。
について、次のいずれかが成り立つときに言う。
 =0
=0

 は
は  の素元の積に分解される。
の素元の積に分解される。
 は整域であるとする。このとき、
は整域であるとする。このとき、
 の素元は、必ず既約である。
の素元は、必ず既約である。
 の既約元は、必ずしも素元とは限らない。
の既約元は、必ずしも素元とは限らない。
 が素元分解環ならば、その既約元は必ず素元である。
が素元分解環ならば、その既約元は必ず素元である。

![% latex2html id marker 924
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-5}] $](img4.png) では
素因数分解は一意的でない。例えば
では
素因数分解は一意的でない。例えば
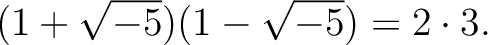
 のイデアルの増大列
のイデアルの増大列
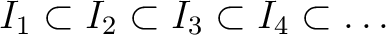
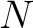 があって、
があって、
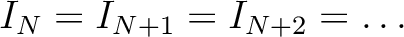
 がネータ環であるとは、
がネータ環であるとは、
 の任意のイデアルが有限個の元で生成される
場合に言う。ネータ環のイデアルの増大列も、必ずどこかで止まることが証明できる。
証明はほとんど同じなので進んで勉強したい人はやってみられると良い。
(余談ながらネータ環は環論において大変重要な対象である。
体上有限生成な環は全てネータ環である。(ヒルベルトの基定理))
の任意のイデアルが有限個の元で生成される
場合に言う。ネータ環のイデアルの増大列も、必ずどこかで止まることが証明できる。
証明はほとんど同じなので進んで勉強したい人はやってみられると良い。
(余談ながらネータ環は環論において大変重要な対象である。
体上有限生成な環は全てネータ環である。(ヒルベルトの基定理))