Next: About this document ...








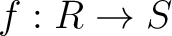 について、
について、
 の同値関係
の同値関係 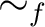 を
を
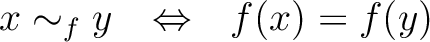
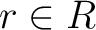 の
の
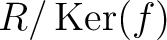 でのクラスを
でのクラスを 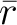 とすると、
次のことが成り立つ。
とすると、
次のことが成り立つ。
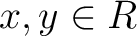 にたいして、
にたいして、
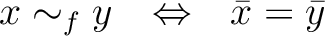
 は
は
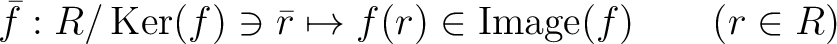
代数では群、加群、環、Lie 環など、いろいろなモノについて それぞれ「準同型定理」がなりたつが、それはすべて次の 単純な事実に基づく:
| 「値による分類」 |
|---|
写像 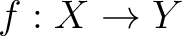 が与えられたとき、 が与えられたとき、
 の行き先でわけることによって の行き先でわけることによって  の元の分類(クラスわけ)ができる。 の元の分類(クラスわけ)ができる。
|
さらに、
| Kernel の重要性 |
|---|
 が環の準同型の場合には、 が環の準同型の場合には、 の値による分類は「差が の値による分類は「差が
 に入るかどうかの
分類」と同じことである。 に入るかどうかの
分類」と同じことである。
|
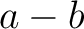 で決まるものであるが、
群の場合には、
で決まるものであるが、
群の場合には、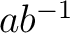 で与える。)
で与える。)
環準同型
![$f: {\mbox{${\mathbb{Z}}$}}[X] \to {\mbox{${\mathbb{Z}}$}}$](img28.svg)

![$X^2+3X+5 \in {\mbox{${\mathbb{Z}}$}}[X]$](img30.svg) の
の  による像を具体的に求めなさい。
による像を具体的に求めなさい。
 の元で、 0 と異なるものを具体的に3つあげなさい。
の元で、 0 と異なるものを具体的に3つあげなさい。