Next: About this document ...






 は
は  から
から  への群としての準同型である。すなわち、
への群としての準同型である。すなわち、

 の元
の元  について成り立つ。
について成り立つ。
 は
は  の積を
の積を  の積にうつす。すなわち、
の積にうつす。すなわち、

 の元
の元  について成り立つ。
について成り立つ。
 は(
は( の)単位元を(
の)単位元を( の)単位元にうつす。すなわち、
の)単位元にうつす。すなわち、

 が与えられたとき、
が与えられたとき、
 の逆写像
の逆写像  は
は  から
から  への
同型になる。
への
同型になる。群(加法群)についての準同型の知識を使うと、次のことは直ちにわかる。
 について、
について、
 が成り立つ。
が成り立つ。
 が全ての
が全ての  に対して成り立つ。
に対して成り立つ。
 について、
について、
 のことを、
のことを、
 の核(Kernel)と呼び、
の核(Kernel)と呼び、
 で書き表す。
で書き表す。


 にたいして、
にたいして、
 は
は  のイデアルである。
のイデアルである。
 は
は  の部分環である。
の部分環である。
環 
![$R[X]$](img1.png) とは、
とは、

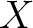 とで生成される
環であった。同様に
とで生成される
環であった。同様に
![$R[X_1,X_2,\dots,X_n]$](img3.png) を定義することができる。
その出自から当然、次の補題が成り立つ
を定義することができる。
その出自から当然、次の補題が成り立つ
 について、
について、
![$R[X][Y]\cong R[X,Y]
$](img4.png) という自然な同型が存在する。
もっと一般に
という自然な同型が存在する。
もっと一般に
![$R[X_1,X_2,\dots,X_n] \cong R[X_1,X_2,\dots,X_{n-1}][X_n]
$](img5.png) がなりたつ。
がなりたつ。
 とその部分環
とその部分環  が与えられているとする。
このとき、任意の
が与えられているとする。
このとき、任意の  の元の
の元の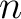 個の組
個の組
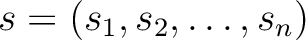 にたいして、
次のような環準同型
にたいして、
次のような環準同型
![$\psi_s[X_1,X_2,\dots,X_n] \to S$](img8.png) が
唯一つ存在する。
が
唯一つ存在する。

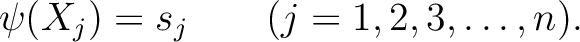
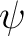 は次のような形で与えられる。
は次のような形で与えられる。
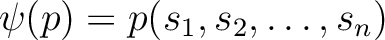
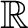
![$[X]$](img14.png) から
から
 への写像
への写像  を、
を、
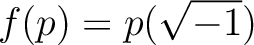
 は写像としてうまく定義されている。
は写像としてうまく定義されている。
 は環の準同型である。
は環の準同型である。
 の像は
の像は
 全体である。
全体である。
 の核は
の核は
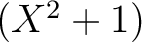
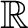
![$[X]$](img14.png) である。
である。