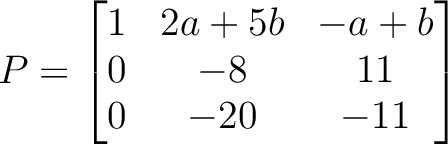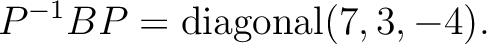Next: About this document ...
言うまでもないことだが、数値的な答だけでは十分ではない。 論理的な説明がもっと大事である。
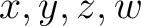 は実数であるとする。
は実数であるとする。
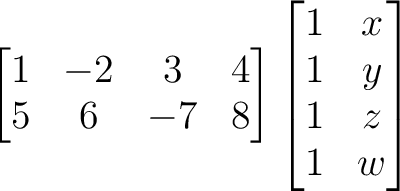
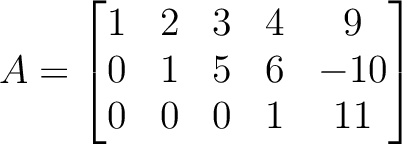
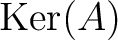 をもとめよ。
をもとめよ。
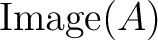 を求めよ。
を求めよ。
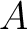 に対する次元定理を、
に対する次元定理を、
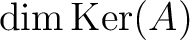 等がこの場合にはどのような値になるかをきちんと当てはめて、書け。
等がこの場合にはどのような値になるかをきちんと当てはめて、書け。
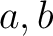 は実数とする。
は実数とする。
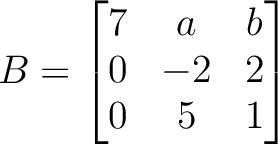
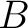 の固有値をすべて求めよ。
の固有値をすべて求めよ。
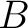 の各固有値に属する固有ベクトルをそれぞれ求めよ。
の各固有値に属する固有ベクトルをそれぞれ求めよ。
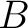 を対角化せよ。
を対角化せよ。
15.1
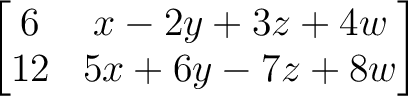
15.2
(1)
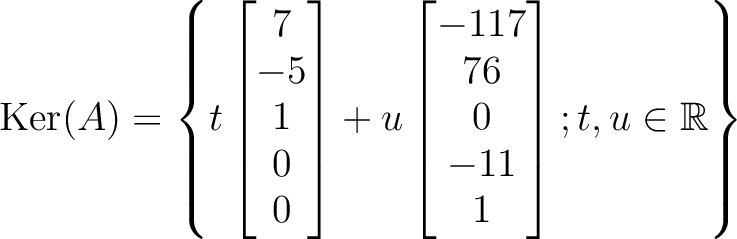
(2)
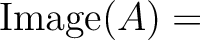
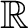
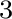 .
.
(3)
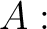
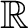
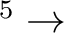
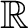
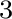
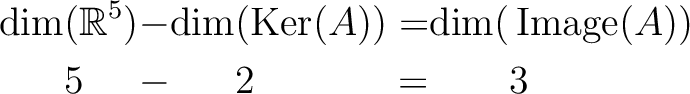
15.3.
(1)
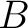 の固有値は
の固有値は 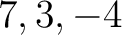 .
.
(2)
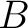 の
の 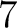 に対応する固有ベクトルは
に対応する固有ベクトルは

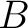 の
の 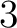 に対する固有ベクトルは
に対する固有ベクトルは
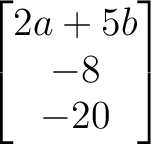 .
.
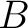 の
の 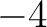 に対応する固有ベクトルは
に対応する固有ベクトルは
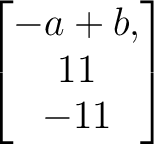 .
.
(3)