Next: About this document ...
今日のテーマ:逆行列
行の数と列の数が同じ行列のことを正方行列というのでした。
◎ 2次行列の逆行列
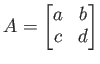 が正則であるための必要十分条件は、
が正則であるための必要十分条件は、
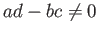 である。
である。
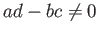 のとき、
のとき、
![]() と書くと、
と書くと、![]() の逆行列は
の逆行列は
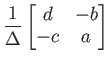
二次行列に限らず、一般のサイズの正方行列 ![]() が逆行列を持つならば、
一次方程式
が逆行列を持つならば、
一次方程式
逆行列をもとめるのは、一次方程式をたくさん解くのと同じことである:
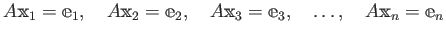
この命題では ![]() のみに言及している。逆の積
のみに言及している。逆の積 ![]() がどうなるかについては
どうしてもちょっとした議論が必要になる。
がどうなるかについては
どうしてもちょっとした議論が必要になる。