Next: About this document ... Up: いくつかの多項式の既約性(例) Previous: 用いること
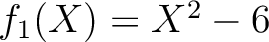 は
は
 上既約である。
上既約である。 上に帰着]
ガウスの補題により、
上に帰着]
ガウスの補題により、
 上既約であることをいえばよい。
もし
上既約であることをいえばよい。
もし 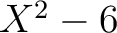 が
が
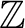 上可約であれば、
次数の関係を考えると、一次式の積に分解する他はないことがわかる。
最高次の係数を比べることにより、それらの一次式は(符号の調整後)モニックである
ことがわかるから、
上可約であれば、
次数の関係を考えると、一次式の積に分解する他はないことがわかる。
最高次の係数を比べることにより、それらの一次式は(符号の調整後)モニックである
ことがわかるから、
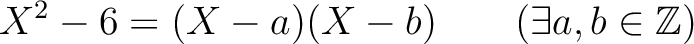
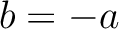 であって、
であって、
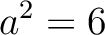
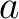 は存在しない(大きさの比較により、
は存在しない(大きさの比較により、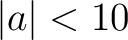 で、
あとは全数調査。もちろんもっと効率的な方法でもよい。)
で、
あとは全数調査。もちろんもっと効率的な方法でもよい。)
(略解2)
ガウスの補題により、
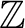 上既約であることをいえばよい。
それには
上既約であることをいえばよい。
それには
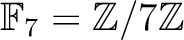 で既約であることを言えば十分。
で既約であることを言えば十分。
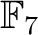 では
では
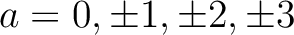 に対して、
に対して、
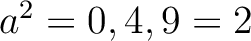 であるから、
であるから、
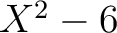 の根は
の根は
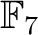 の中にはない。
の中にはない。
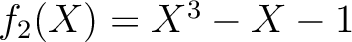 は
は
 上既約である。
上既約である。
(略解1) [
 上に帰着]
上に帰着]
ガウスの補題により、
 上既約であることをいえばよい。
上既約であることをいえばよい。
もし 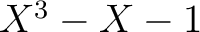 が
が
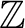 上可約であれば、
上可約であれば、
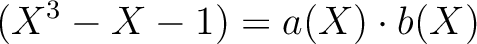
![$a,b\in{\mbox{${\mathbb{Z}}$}}[X]$](img41.png) で、定数でないものが存在する。
次数の関係により、
で、定数でないものが存在する。
次数の関係により、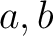 のうち一方は1次式、もう一方は2次式であり、
さらに係数の関係により、
のうち一方は1次式、もう一方は2次式であり、
さらに係数の関係により、
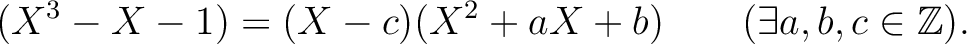
 は
は 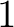 の約数、すなわち
の約数、すなわち 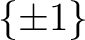 の
元でなければならない。
の
元でなければならない。
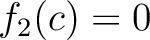 でなければならないが、それは不可能。
でなければならないが、それは不可能。
(略解2)[
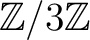 上に帰着]
上に帰着]
ガウスの補題により、
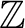 上既約であることをいえばよい。
そのためには、
上既約であることをいえばよい。
そのためには、
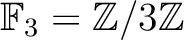 上既約ならば十分である。
上既約ならば十分である。
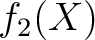 は
は
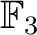 に根をもたないことがわかるから、
に根をもたないことがわかるから、
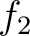 は
は
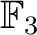 上既約である。(根をもたない 2次 or 3次の多項式は既約。)
上既約である。(根をもたない 2次 or 3次の多項式は既約。)
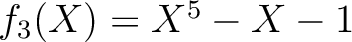 は
は
 上既約である。
上既約である。
(略解)[
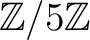 上に帰着:
上に帰着:
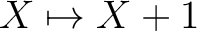 に関する不変性を使う]
に関する不変性を使う]
ガウスの補題により、
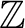 上既約であることをいえばよい。
上既約であることをいえばよい。
それには (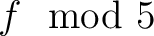 が)
が)
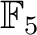 上既約であることを示せば十分である。
以下
上既約であることを示せば十分である。
以下
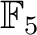 で議論する。
で議論する。
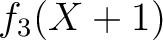 |
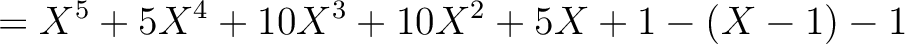 |
|
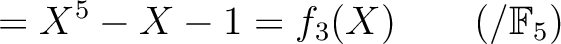 |
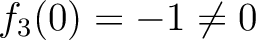 であることから、
(2.1)式により、
であることから、
(2.1)式により、
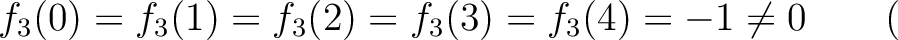 in
in 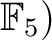
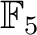 上では
上では 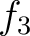 は1次の因子をもたない。
は1次の因子をもたない。
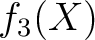 が仮に 2次の既約因子
が仮に 2次の既約因子 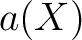 を持つとする。
を持つとする。
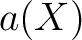 はモニックであると仮定してよい。(2.1)式により、
はモニックであると仮定してよい。(2.1)式により、
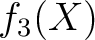 は
は 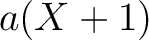 をも既約因子に持つ。
同様にして、
をも既約因子に持つ。
同様にして、
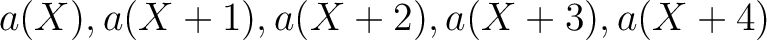
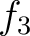 の2次の既約因子であることがわかる。
素因子分解の一意性と、これらがモニックであることとにより、
これら5つの多項式のうち少なくとも2つは等しい。
の2次の既約因子であることがわかる。
素因子分解の一意性と、これらがモニックであることとにより、
これら5つの多項式のうち少なくとも2つは等しい。

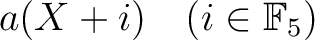 がすべて等しいことを意味している。
(演習問題:
がすべて等しいことを意味している。
(演習問題:
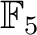 は加法的に
は加法的に 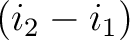 で生成されることを用いる。)
とくに
で生成されることを用いる。)
とくに
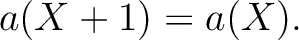
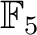 上の
上の 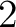 次式は存在しない。(練習問題)
次式は存在しない。(練習問題)
(略解2) [
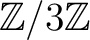 上に帰着:コンピュータを使い全数調査]
ガウスの補題により、
上に帰着:コンピュータを使い全数調査]
ガウスの補題により、
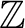 上既約であることをいえばよい。
それには (
上既約であることをいえばよい。
それには (
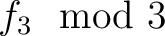 が)
が)
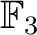 上既約であることを示せば十分である。
以下
上既約であることを示せば十分である。
以下
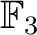 で議論する。
で議論する。
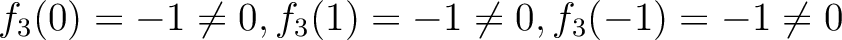 であるから、
であるから、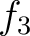 は
は
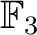 上1次の因数をもたない。
上1次の因数をもたない。
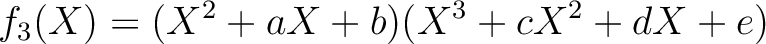
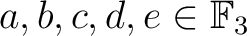 を機械で総当りに求めると、
そのようなものは存在しないことがわかる。
(総当りに必要な組み合わせは
を機械で総当りに求めると、
そのようなものは存在しないことがわかる。
(総当りに必要な組み合わせは 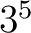 とおり。)
よって
とおり。)
よって 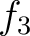 は既約である。
は既約である。
後半は次のように処理すると計算をかなり減らせる:
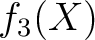 を
を 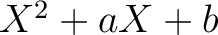 で割った余り
で割った余り

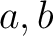 の値として
の値として
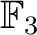 のどれをとっても 0 にはならない。
(
のどれをとっても 0 にはならない。
(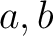 の値の選び方は
の値の選び方は 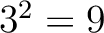 とおり。このぐらいならうまく整理しながらやれば
人間でも可能。)
とおり。このぐらいならうまく整理しながらやれば
人間でも可能。)