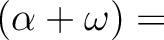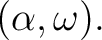Next: About this document ...
![% latex2html id marker 1424
$ \alpha=\sqrt[3]{11}$](img1.png) ,
,
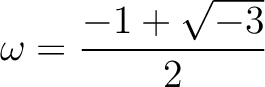 とおくとき、
とおくとき、
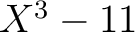 は
は
 上既約だろうか?
上既約だろうか?
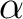 の
の
 上の共役をすべて求めなさい。
上の共役をすべて求めなさい。

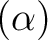 ,
,

 のそれぞれは
のそれぞれは
 のガロア拡大であるか、
理由をつけて述べなさい。
のガロア拡大であるか、
理由をつけて述べなさい。

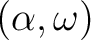 は
は
 上のガロア拡大だろうか?
上のガロア拡大だろうか?
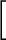

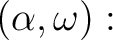

![$]$](img11.png) を求めなさい。
を求めなさい。

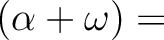

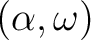 であることを示しなさい。
であることを示しなさい。
[解答]
(1) 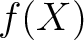 は
は
 上既約である。
これを証明しよう。背理法で
上既約である。
これを証明しよう。背理法で 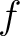 が
が
 可約だとする。 命題5.1(ガウスの補題) により
可約だとする。 命題5.1(ガウスの補題) により
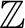 上でも可約である。
上でも可約である。
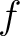 は
は 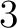 次だから
次だから  次の
次の
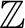 係数の因数を持つことになる。
命題5.4により
係数の因数を持つことになる。
命題5.4により 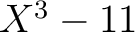 の因数はモニック。ゆえに、
の因数はモニック。ゆえに、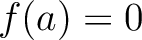 なる
整数
なる
整数 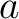 が存在することになる。
が存在することになる。
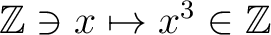 は単調増加
かつ、
は単調増加
かつ、
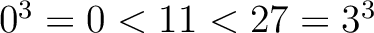 により、
により、 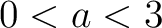 . つまり
. つまり 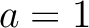 or
or 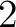 であるが、
これらは
であるが、
これらは 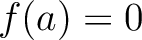 を満たさないから矛盾。
を満たさないから矛盾。
[別解] 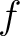 が
が
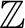 上で可約ならば、
上で可約ならば、
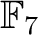 上でも可約なはず。
すなわち
上でも可約なはず。
すなわち 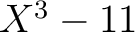 は
は
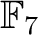 上で根を持つことになる。ところが
上で根を持つことになる。ところが
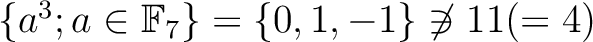 (in
(in
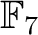 .) ゆえ、矛盾。
.) ゆえ、矛盾。
(2)
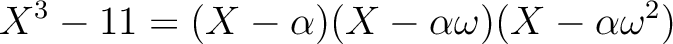
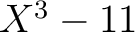 は
は
 上既約であるから、
上既約であるから、
 が
が 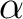 の
の
 上の共役である。
上の共役である。
(3)

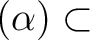
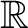 かつ
かつ
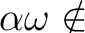
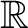 により、
により、
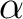 の共役の一つ
の共役の一つ
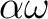 は
は

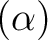 に含まれない。
ゆえに、
に含まれない。
ゆえに、

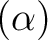 は
は
 の正規拡大ではない。もちろん、ガロア拡大でもない。
の正規拡大ではない。もちろん、ガロア拡大でもない。
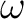 の
の
 上の最小多項式は
上の最小多項式は
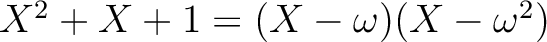 であるから、
であるから、
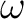 の
の
 上の共役は
上の共役は
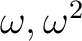 の二つ。
これらは
の二つ。
これらは

 に含まれるから、
に含まれるから、

 は
は
 上の正規拡大である。
上の正規拡大である。
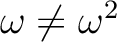 だから
だから 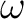 は
は
 上分離的でもある。
ゆえに、
上分離的でもある。
ゆえに、

 は
は
 のガロア拡大である。
のガロア拡大である。
(4)
(3)と同様の考察により、

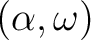 は
は
 のガロア拡大である
ことがわかる。
のガロア拡大である
ことがわかる。
(5)

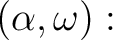

![$\displaystyle ]
=[$](img41.png)

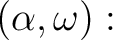

![$\displaystyle (\alpha)] [$](img42.png)

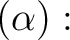

![$\displaystyle ]
=3[$](img44.png)

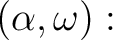

![$\displaystyle (\alpha)].
$](img45.png)
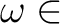

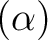 か否かによって、
か否かによって、
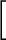

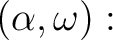

![$(\alpha)]$](img47.png) は
は 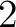 か
か 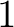 かのいづれかである。他方、
かのいづれかである。他方、
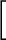

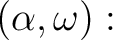

![$\displaystyle ]
=[$](img41.png)

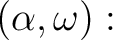

![$\displaystyle (\omega)] [$](img48.png)

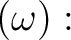

![$\displaystyle ]
=2[$](img50.png)

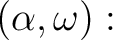

![$\displaystyle (\omega)].
$](img51.png)

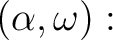

![$]$](img11.png) は
は  の倍数でなければならない。
ゆえに、
の倍数でなければならない。
ゆえに、
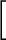

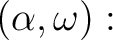

![$]=6$](img52.png) .
.
(もしくは:
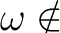
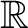 かつ
かつ

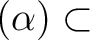
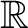 ゆえ
ゆえ
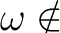

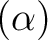 . よって、
. よって、
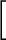

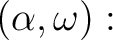

![$(\alpha)]=2$](img54.png) . とやってもよい。
)
. とやってもよい。
)
(6)
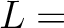

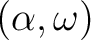 とおこう。
とおこう。 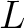 の元は必ず
の元は必ず
 |
(B) |
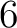 つの元は一次独立でなければならない。
すなわち、これら
つの元は一次独立でなければならない。
すなわち、これら 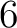 つの元は
つの元は 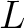 の
の
 上のベクトル空間としての基底である。
上のベクトル空間としての基底である。
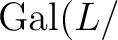

 の元は
の元は 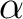 の行き先(
の行き先(
 の
3とおり)と
の
3とおり)と
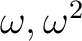 の行き先(2とおり)
の都合
の行き先(2とおり)
の都合 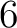 通りで定まる。(命題9.4 により、これら
通りで定まる。(命題9.4 により、これら 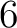 つの可能性はすべて
ガロア群の元として実現されねばならない。)
つの可能性はすべて
ガロア群の元として実現されねばならない。)
ガロア群の元 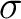 が
が
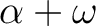 を動かさないとすると、
を動かさないとすると、
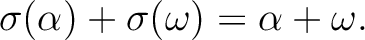
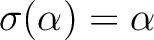 or
or 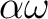 or
or 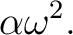
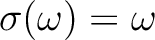 or
or 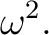
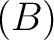 の6つの元が一次独立なことから、必然的に
の6つの元が一次独立なことから、必然的に
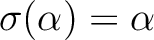 かつ
かつ
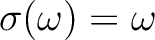 がわかる。すなわち、
がわかる。すなわち、
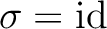 .
よって、
.
よって、
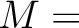

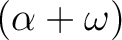 にガロア対応で対応する
にガロア対応で対応する
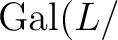

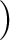 の
部分群(
の
部分群( 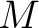 の固定群) は
の固定群) は
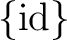 で、
これは
で、
これは

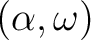 の固定群と等しい。
ガロア対応が全単射的であること(ガロア理論の基本定理)から、
の固定群と等しい。
ガロア対応が全単射的であること(ガロア理論の基本定理)から、