Next: About this document ...
今日のテーマ:体の同型を数える。
体  上の分離代数的な元
上の分離代数的な元
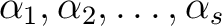 に対して、
に対して、
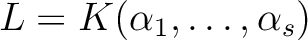 の元
の元 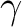 が存在して、
が存在して、
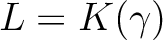 とできるのであった。
この
とできるのであった。
この 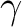 は
は  上分離的に取れる。
上分離的に取れる。
体  の拡大体
の拡大体 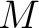 と
と ![]() とがあるとき、
とがあるとき、 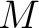 から
から ![]() への
への  -同型
の数を数えることにより、
-同型
の数を数えることにより、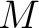 の性質がある程度分かる。本日はそんな話。
の性質がある程度分かる。本日はそんな話。
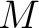 から
から  -同型(環としての準同型で、
-同型(環としての準同型で、
 上では恒等写像と等しいもの)の全体の集合を
上では恒等写像と等しいもの)の全体の集合を
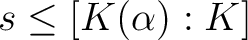
まず 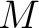 が
が  の単純拡大のときから
考えてみよう。
の単純拡大のときから
考えてみよう。
 上の代数的数
上の代数的数  の拡大体
の拡大体  -同型はちょうど
-同型はちょうど ![% latex2html id marker 1023
$ s\leq [K(\alpha):K]$](img15.png) で、等号は次の二つの条件がともに成り立つとき、
そしてそのときに限りなりたつ。
で、等号は次の二つの条件がともに成り立つとき、
そしてそのときに限りなりたつ。
 上分離的である。
上分離的である。
上の補題は、
![]() が十分大きいときには
が十分大きいときには
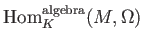 の
元の数が分離性の判定に使えることを示唆している。
上の補題を何度も用いることにより、次のことが証明できる。
の
元の数が分離性の判定に使えることを示唆している。
上の補題を何度も用いることにより、次のことが証明できる。
 上代数的な元
上代数的な元
 の拡大体
の拡大体
![% latex2html id marker 1052
$\displaystyle \operatorname{Hom}_K^{\operatorname{alg}}(M,\Omega)\leq [M:K].
$](img19.png)
 上分離的で、
上分離的で、
ちょっとトリッキーだが、次のことにも注意しておこう。
 の拡大体
の拡大体 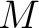 のどれかひとつの元
のどれかひとつの元  上非分離的であるならば、
上非分離的であるならば、
![$\displaystyle \operatorname{Hom}_K^{\operatorname{alg}}(M,\Omega)< [M:K].
$](img20.png)
 上代数的な元
上代数的な元
 上分離的ならば
上分離的ならば
「大きな体」![]() に頼ってばかりいると面倒である。
これを排除するために(もちろん他の理由もあるが次のようなものを考える。
に頼ってばかりいると面倒である。
これを排除するために(もちろん他の理由もあるが次のようなものを考える。
 上の代数拡大体
上の代数拡大体  上正規拡大であるとは、
上正規拡大であるとは、
 上の最小多項式が必ず
上の最小多項式が必ず
 の分離的でかつ正規な代数拡大をガロア拡大と呼ぶ。
の分離的でかつ正規な代数拡大をガロア拡大と呼ぶ。
体  のガロア拡大
のガロア拡大 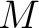 が与えられたとすると、
上で
が与えられたとすると、
上で ![]() として使っていたものの代わりに
として使っていたものの代わりに 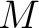 自身を使えることが
わかる。
自身を使えることが
わかる。
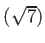 は
は