Next: About this document ...
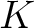 に対して
に対して 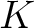 を含む代数的閉体が存在する。(2)
を含む代数的閉体が存在する。(2)
「任意の体 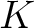 に対して
に対して 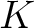 を含む代数的閉体が存在する。」
(無印だが、以下では便宜上「(1)」と呼ぶことにする)
において、
次の「主張2」に言及した。
を含む代数的閉体が存在する。」
(無印だが、以下では便宜上「(1)」と呼ぶことにする)
において、
次の「主張2」に言及した。
| [ | ||
|---|---|---|
l]主張2
体 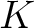 とその拡大体 とその拡大体 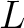 が、次の性質を満たしたとする。 が、次の性質を満たしたとする。
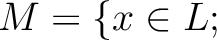 $x$ は $K$ 上代数的 $x$ は $K$ 上代数的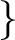
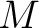 は は 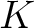 を含む代数閉体である。 を含む代数閉体である。
|
今回は、分離性の知識を用いて、
次のこと(主張2s)を証明する。
(議論をいくらか簡潔にするため、
全体は大きな代数的閉体 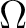 に埋め込まれている
と考えることにする。
に埋め込まれている
と考えることにする。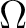 としては(1)ですでに証明した
としては(1)ですでに証明した 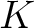 の代数的
閉包(議論としてはそれで十分なことを確認できるが、
それで物足りなければ
の代数的
閉包(議論としてはそれで十分なことを確認できるが、
それで物足りなければ 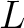 の代数的閉包)を用いてもよい。)
の代数的閉包)を用いてもよい。)
| [ |
|---|
l]主張2s
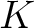 とその拡大体 とその拡大体 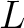 が、主張2 の性質(※)を満たしたとする。
このとき、 が、主張2 の性質(※)を満たしたとする。
このとき、
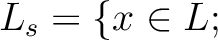 $x$ は $K$ 上分離代数的 $x$ は $K$ 上分離代数的
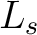 は は 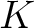 上分離代数的な ( 上分離代数的な (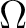 の)元をすべて
含む。つまり、 の)元をすべて
含む。つまり、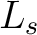 は は 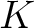 の分離閉包である。 の分離閉包である。
|
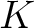 の標数が 0 なら、分離性の仮定は常に満足されるから、
そのときには主張 2 も正しいことがわかる。
の標数が 0 なら、分離性の仮定は常に満足されるから、
そのときには主張 2 も正しいことがわかる。
[主張 2s の証明]
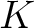 上分離代数的な元
上分離代数的な元 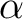 をとる。
をとる。
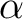 の最小多項式を
の最小多項式を 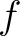 と書き、
と書き、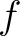 の根を
の根を
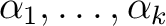 と置くと、
と置くと、
 は
は 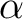 の
の 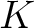 上の共役の全体
と等しく、
上の共役の全体
と等しく、
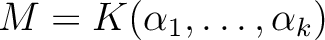 は
は
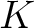 の有限個の分離的な元による拡大であるから、
の有限個の分離的な元による拡大であるから、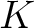 の単純拡大である
(No.6, 系6.9)。
すなわち、 ある
の単純拡大である
(No.6, 系6.9)。
すなわち、 ある 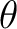 が存在して、
が存在して、
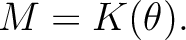
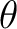 の 最小多項式
の 最小多項式 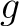 は仮定(※)により少なくとも一つの根
は仮定(※)により少なくとも一つの根
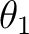 を
を 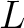 にもつ. 「ガロア理論の第一歩」により、
にもつ. 「ガロア理論の第一歩」により、
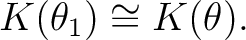
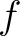 は
は 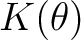 上一次式の積に分解されるから、
上一次式の積に分解されるから、
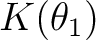 でも
そうである。つまり、
でも
そうである。つまり、 の根
の根
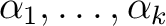 はすべて
はすべて 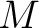 に
属する。
に
属する。
ARRAY(0x5632a1235b60)