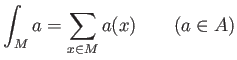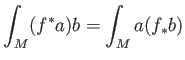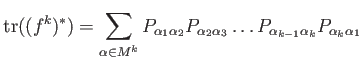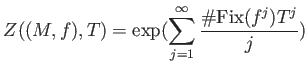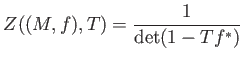Congruent zeta functions. No.11
Yoshifumi Tsuchimoto
Let 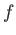 be a self map
be a self map 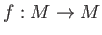 of a set
of a set 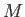 .
It defines a (discrete) dynamical system
.
It defines a (discrete) dynamical system 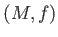 .
.
To explain the basic idea, we first examine the case where 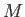 is a
finite set.
is a
finite set.
We put
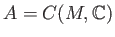 , the set of
, the set of
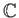 -valued functions on
-valued functions on 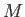 .
.
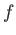 defines a pull-back of functions:
defines a pull-back of functions:
and push-forward:
(It might be better to treat the push-forward as above
as a push-forward of measures.)
We note also that any element of 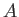 admits an integration
admits an integration
(which is a integration with respect to the counting measure.)
PROPOSITION 11.1
We have
In other words, 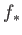 is the adjoint of
is the adjoint of 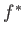 .
.
DEFINITION 11.3
We define the set
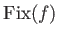
as the set of fixed points of
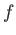
. Namely,
PROPOSITION 11.4
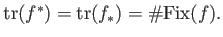
It should be noted that
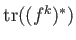 may be comuted using a “path-integral”-like
formula.
may be comuted using a “path-integral”-like
formula.
DEFINITION 11.5
We define the Artin-Mazur zeta function of a dynamical system
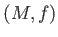
as
![]() be a self map
be a self map ![]() of a set
of a set ![]() .
It defines a (discrete) dynamical system
.
It defines a (discrete) dynamical system ![]() .
.
![]() is a
finite set.
is a
finite set.
![]() , the set of
, the set of
![]() -valued functions on
-valued functions on ![]() .
.
![]() defines a pull-back of functions:
defines a pull-back of functions:
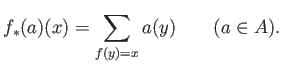
![]() admits an integration
admits an integration