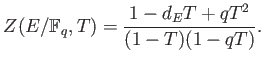Congruent zeta functions. No.10
Yoshifumi Tsuchimoto

There is diverse deep theories on elliptic curves.
Let 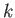 be a field of characteristic
be a field of characteristic
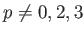 .
We consider a curve
.
We consider a curve 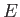 in
in 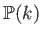 of the following type:
of the following type:
(The equation, of course, is written in terms of inhomogeneous coordinates.
In homogeneous coordinates, the equation is rewritten as:
Such a curve is called an elliptic curve.
It is well known (but we do not prove in this lecture) that
THEOREM 10.1
The set 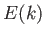 of
of 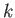 -valued points of the elliptic curve
-valued points of the elliptic curve 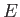 carries a
structure of an abelian group. The addition is so defined that
carries a
structure of an abelian group. The addition is so defined that
We would like to calculate congruent zeta function of 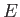 .
.
For the moment, we shall be content to prove:
See [1] for more detail and a further story.
The following proposition
is a special case of the Weil conjecture.
(It is actually a precursor of the conjecture)
PROPOSITION 10.3 (Weil)
Let 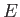 be an elliptic curve over
be an elliptic curve over
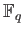 . Then we have
. Then we have
where 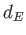 is an integer which satisfies
is an integer which satisfies
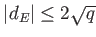 .
.
Note that for each 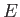 we have only one unknown integer
we have only one unknown integer 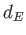 to
determine the Zeta function.
So it is enough to compute
to
determine the Zeta function.
So it is enough to compute
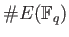 to compute the Zeta function of
to compute the Zeta function of 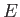 . (When
. (When 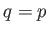 then one may use
Proposition 10.2 to do that.)
then one may use
Proposition 10.2 to do that.)
EXERCISE 10.1
compute the congruent zeta function
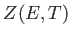
for an elliptic curve
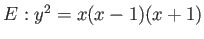
.
![]()
![]() be a field of characteristic
be a field of characteristic
![]() .
We consider a curve
.
We consider a curve ![]() in
in ![]() of the following type:
of the following type:
![]() .
.