PROOF..
We first prove the lemma when
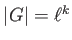
for some prime number
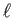
.
In such a case Euler-Lagrange theorem implies that any element
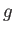
of
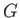
has an order
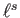
for some
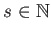
,
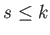
.
Let
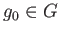
be an element which has the largest order
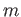
.
Then we see that any element of
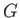
satisfies the equation
Since
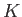
is a field, there is at most
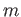
solutions to the equation.
Thus
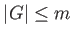
. So we conclude that
the order
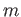
of
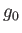
is equal to
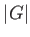
and that
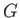
is generated by
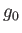
.
Let us proceed now to the general case. Let us factorize the order 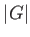 :
:
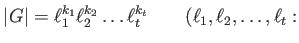
prime,
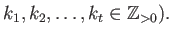
Then
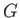
may be decomposed into product of
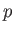
-subgroups
By using the first step of this proof we see that each
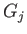
is
cyclic. Thus we conclude that
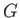
is also a cyclic group.
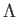
![]()
![]() ,
,
![]() .
To construct
.
To construct
![]() for
for ![]() ,
,
![]() :
: