Next: About this document ...
今日のテーマ: 対称行列の標準形
今回は複素数の性質、特に複素共役の性質を用いる。
行列 ![]() に対して、
に対して、 ![]() で
で
![]() のそれぞれの成分の複素共役をとった行列を指す。
行列
のそれぞれの成分の複素共役をとった行列を指す。
行列 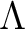 に対して
に対して
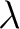 (サイズ的に和や積が定義される限り)
(サイズ的に和や積が定義される限り)
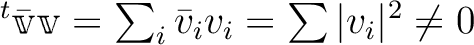 とおく。定義により、
ある
とおく。定義により、
ある
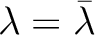 が
存在して、
が
存在して、
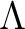 .
その複素共役をとることにより、
.
その複素共役をとることにより、
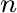 を得る。
を得る。
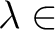 を2通りに計算してみよう。一方では
を2通りに計算してみよう。一方では
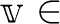 |
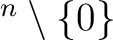 |
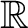 ところが
ところが
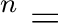 であるから、
であるから、
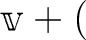 すなわち
すなわち 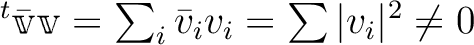 は実数である。
は実数である。
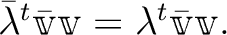
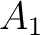 から
から
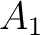 への
一次写像と同一視する。
への
一次写像と同一視する。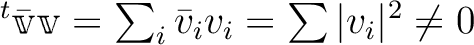 をとる。
命題
をとる。
命題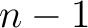
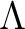 となる
となる
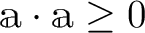
 が存在する。
が存在する。






 と、
と、

 の正規直交基底をとってきて並べたてできた行列を
の正規直交基底をとってきて並べたてできた行列を

 は
は  次の対称行列)という具合に書ける。
次の対称行列)という具合に書ける。
 に対して帰納法を用いればよい。
に対して帰納法を用いればよい。
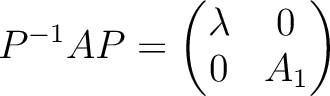
参考:
 .
.
エルミート内積を持つ複素ベクトル空間を 複素計量ベクトル空間 と呼ぶ。
複素計量ベクトル空間でも、シュミットの直交化法に代表されるような技法・定理が 同様にある。