Next: About this document ...
今日のテーマ: 直交射影を表す行列(2)
ベクトル空間 ![]() の基底
の基底
![]() が与えられたとき、
が与えられたとき、
![]() の元
の元
![]() は
は
![]()
![]() の元
の元
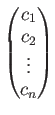 と
同一視されるのでした。
と
同一視されるのでした。 ![]() が計量ベクトル空間で、
が計量ベクトル空間で、![]() が
正規直交基底(ONB) ならば、
が
正規直交基底(ONB) ならば、![]() の内積は
の内積は
![]()
![]() の標準内積に対応します。
の標準内積に対応します。
![]()
![]() の元
の元
![]() の標準内積は、行列の積を用いて
の標準内積は、行列の積を用いて
![]() と書くことができることにも注意しておきます。
と書くことができることにも注意しておきます。
先週に引き続き以下でも、標準的な内積を用いる。
![]() の像(Image)と核(Kernel)の定義にも注意しておこう。
の像(Image)と核(Kernel)の定義にも注意しておこう。
![]()
![]()
![]() に対して、
に対して、
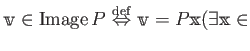
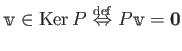
正方行列 ![]() について、つぎのことにも注意しておく。(上記補題の
幾何学的な言い換え)
について、つぎのことにも注意しておく。(上記補題の
幾何学的な言い換え)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()