Next: About this document ...
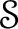 があるとする。もし
があるとする。もし
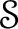 の任意の鎖が
の任意の鎖が
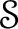 内に上界を持つとすると、
内に上界を持つとすると、
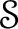 は極大元を持つ。
は極大元を持つ。Zornの補題を使って、次のことを示せる:
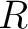 とそのイデアル
とそのイデアル 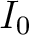 で、
で、
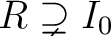 を満たすものがあったとする。
このとき、
を満たすものがあったとする。
このとき、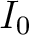 を含む
を含む 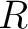 の極大イデアルが存在する。
とくに、
の極大イデアルが存在する。
とくに、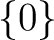 でない環
でない環 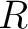 は極大イデアルを持つ。
は極大イデアルを持つ。
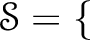 $I_0$ を含む $R$ の(両側)イデアルのうち $R$ 自身以外からなるもの
$I_0$ を含む $R$ の(両側)イデアルのうち $R$ 自身以外からなるもの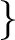
 は
は 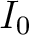 を含むので空ではない。
を含むので空ではない。
 は包含関係により半順序集合である。
は包含関係により半順序集合である。
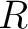 の極大イデアルを見つけることは
の極大イデアルを見つけることは
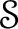 の極大元を見つけることと同じである。
の極大元を見つけることと同じである。
Zornの補題を適用するために、
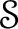 の空でない全順序部分集合
の空でない全順序部分集合
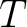 をとる。
をとる。
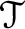 に上界が存在することを示す必要がある。
つまり、イデアル
に上界が存在することを示す必要がある。
つまり、イデアル
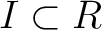 が存在して、
それは
が存在して、
それは
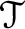 のどの要素より以上であり、
しかも
のどの要素より以上であり、
しかも 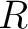 よりは厳密に小さいことを示す必要がある。
よりは厳密に小さいことを示す必要がある。
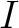 を
を
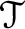 の全てのイデアルの和集合とする。
の全てのイデアルの和集合とする。
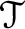 は少なくともひとつ元を持ち、
それは
は少なくともひとつ元を持ち、
それは 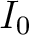 を含んでいるので、和集合
を含んでいるので、和集合 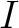 も
も 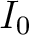 を含み、
とくに空集合ではない。
を含み、
とくに空集合ではない。
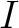 がイデアルであることを示すため、
がイデアルであることを示すため、 と
と 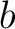 を
を 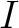 の元とすると、
ふたつのイデアル
の元とすると、
ふたつのイデアル
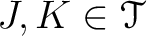 が存在し、
が存在し、
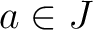 であり、
であり、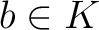 ある。
ある。
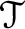 は全順序であったので、
は全順序であったので、
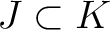 または
または
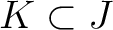 である。
前者の場合は、
である。
前者の場合は、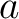 も
も 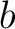 もともに
もともに 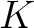 の元であり、
和
の元であり、
和 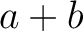 も
も 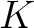 の元である。
よって、
の元である。
よって、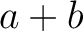 は
は 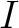 の元である。
後者の場合は、
の元である。
後者の場合は、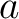 も
も 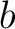 もともに
もともに 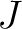 の元であるから、
同様に
の元であるから、
同様に 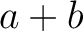 は
は 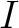 の元である。さらに、任意の
の元である。さらに、任意の 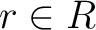 に対して、
に対して、
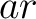 と
と 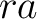 は
は 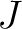 の元であるから、
の元であるから、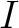 の元でもある。
以上により、
の元でもある。
以上により、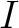 は
は 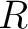 のイデアルであることが分かった。
のイデアルであることが分かった。
そして、イデアルが 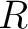 と一致することは
と一致することは 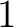 を含むことと同値である。
そこで、
を含むことと同値である。
そこで、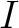 が
が 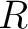 に等しいと仮定すると、それは
に等しいと仮定すると、それは 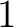 を含み、
を含み、
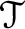 のある要素が
のある要素が 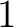 を含むことになり、それは
を含むことになり、それは 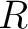 と一致する。
しかし、これは
と一致する。
しかし、これは
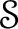 から
から 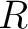 を除いていたことに矛盾する。
を除いていたことに矛盾する。
Zornの補題の条件は確認できたので、
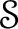 には極大元が存在する。
言い換えると、
には極大元が存在する。
言い換えると、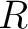 には極大イデアルが存在する。
には極大イデアルが存在する。
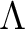
上のように、Zorn の補題の適用時には、 ある一つの集合の部分集合の全体あるいは一部(この場合は全体とは異なるイデアル) を使用することも多い。
Zorn の補題の証明の概略。
| [ |
|---|
l]Zorn の補題
順序集合 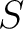 があるとする。もし があるとする。もし 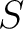 の任意の鎖が の任意の鎖が 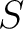 内に上界を持つとすると、 内に上界を持つとすると、
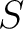 は極大元を持つ。もっと強く、 は極大元を持つ。もっと強く、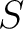 の任意の元 の任意の元 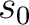 に対して、 に対して、
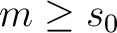 を満たすような
を満たすような 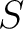 の極大元 の極大元 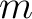 が存在する。 が存在する。
|
以下では 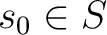 を固定し、補題の後半部分を証明する。
を固定し、補題の後半部分を証明する。
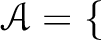 $s_0$ を元として含むような $S$ の鎖
$s_0$ を元として含むような $S$ の鎖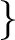
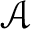 は包含関係に関して順序集合をなす。
は包含関係に関して順序集合をなす。
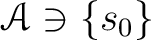 よって
よって
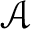 は空ではない。
は空ではない。
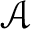 の任意の鎖
の任意の鎖
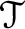 は上限(=最小上界)を持つ。
は上限(=最小上界)を持つ。
さて、
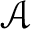 の任意の元
の任意の元 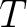 をとってくる。
をとってくる。
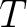 は
は 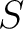 の鎖であるから、仮定により
の鎖であるから、仮定により 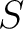 内に上界
内に上界 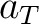 を持つ。
を持つ。
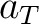 が
が 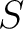 の極大元ならば話は終わりであるから、
の極大元ならば話は終わりであるから、
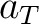 は極大ではないとしてよい。したがって、
ある
は極大ではないとしてよい。したがって、
ある 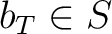 が存在して、
が存在して、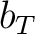 は
は 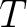 のどの元よりも大きい。
そこで、おのおのの
のどの元よりも大きい。
そこで、おのおのの
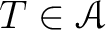 に対してそのような
に対してそのような 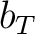 を選び、写像
を選び、写像
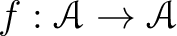 を
を
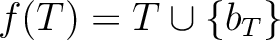
(3)  は
は
 から
から
 への増加写像である。
への増加写像である。
今の場合、 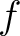 は狭義増加者像であるから、次の Bourbakiの補題に反する。
は狭義増加者像であるから、次の Bourbakiの補題に反する。
| [ |
|---|
l]Bourbakiの補題
順序集合 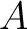 があるとする。
もし があるとする。
もし
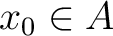 が存在して、 が存在して、
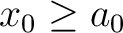 かつ かつ
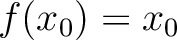 である。 である。
|
Bourbaki の補題の証明の概略。
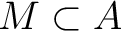 が
が 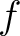 -認容であるというのを
-認容であるというのを
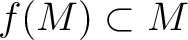
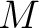 の任意の鎖
の任意の鎖 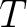 に対して、
に対して、
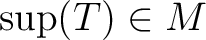
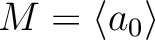 を,「
を,「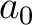 をふくむ
をふくむ 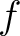 -認容な
-認容な 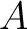 の部分集合のうち
最小のもの」として定義する。
の部分集合のうち
最小のもの」として定義する。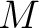 は
は 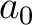 を含む
を含む 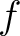 -認容な
-認容な 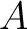 の部分集合の
全体の共通部分であり、「
の部分集合の
全体の共通部分であり、「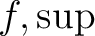 を作用として
を作用として 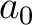 で生成されたような集合」
と思っても差し支えない。
この証明の核心はつぎのことである。
で生成されたような集合」
と思っても差し支えない。
この証明の核心はつぎのことである。
| [ |
|---|
l]証明の核心
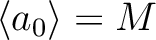 自身も全順序集合(つまり、鎖)である。 自身も全順序集合(つまり、鎖)である。
|
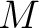 自体が上限
自体が上限 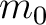 をもち、
をもち、
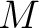 の
の 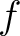 -認容性から
-認容性から 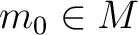 である。
である。
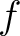 の増加性から
の増加性から
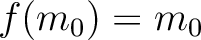 すなわち Bourbaki の補題の
すなわち Bourbaki の補題の 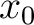 としては
としては
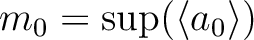 を取れば良いことがわかるという寸法である。
を取れば良いことがわかるという寸法である。
では「核心」の証明はというと、以下 CM ...じゃなくて次ページ。
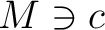 が extreme
が extreme
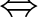
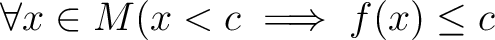 で、「extreme な元」を定義する。
で、「extreme な元」を定義する。
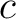 に対して、
に対して、
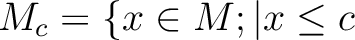 or
or 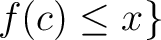 と定義すると、
と定義すると、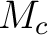 自身も
自身も 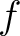 -認容なことがわかり、したがって
-認容なことがわかり、したがって 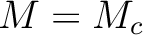 .
.
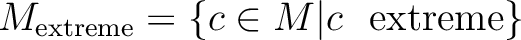 と定義すると、
これもまたもや
と定義すると、
これもまたもや  -認容であることがわかって、
-認容であることがわかって、
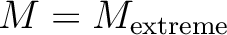
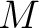 は全順序集合であることがわかる。
は全順序集合であることがわかる。
という具合。詳しくは成書をご覧いただきたい。
この稿では
S. Lang Real and functional analysis third edition (GTM)
を参考にした。