代数学III要約 No.12

定理 12.1   正の整数 $n$ に対して、$z^n=1$ を満たす複素数 $z$ はちょうど $n$個存在する。 それらは

$$\exp(\frac{2 \pi k\sqrt{-1}}{n}) \qquad (k=0,1,2,\dots,n-1)$$

であり、これらを複素平面上で順に線分で結ぶと単位円に内接し、 $1$ をひとつの頂点とする正 $n$ 角形ができる。

命題 12.2   一般に、体 $K$ と正の整数 $n$ に対して、

$$\{x\in K; x^n=1\}$$

は乗法に関して群をなし、その位数は $n$ 以下である。

定義 12.3   体 $K$ に対して、$n$ 乗して初めて $1$ になるような $K$ の元を ($K$ における)$1$ の 原始 $n$ 乗根と呼ぶ。

命題 12.4   ${\mathbb{C}}$ における $1$ の原始 $n$ 乗根 を $\zeta_n$ と書くと、 $\mbox{${\mathbb{Q}}$}$$(\zeta_n)$ は $\mbox{${\mathbb{Q}}$}$ のガロア拡大であり、 ガロア群 $\operatorname{Gal}($$\mbox{${\mathbb{Q}}$}$$(\zeta_n)/$$\mbox{${\mathbb{Q}}$}$$)$ は ${\mbox{${\mathbb{Z}}$}}/n{\mbox{${\mathbb{Z}}$}}$ の乗法群 $({\mbox{${\mathbb{Z}}$}}/n{\mbox{${\mathbb{Z}}$}})^\times$ と同型である。

命題 12.5   $p$ が素数の時、 $({\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}})^\times$ は巡回群である。

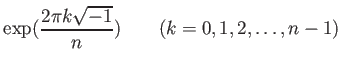
ガロア群がアーベル群(可換群)であるとき、アーベル拡大と呼ばれる。 上の    $\mbox{${\mathbb{Q}}$}$$(\zeta_n)$ は $\mbox{${\mathbb{Q}}$}$ のアーベル拡大の一例である。 実はつぎの驚くべき定理が成り立つ。

定理 12.6 (クロネッカー・ウエーバー)   $\mbox{${\mathbb{Q}}$}$ のアーベル拡大は必ずある円分体 $\mbox{${\mathbb{Q}}$}$$(\zeta_n)$ の部分体である。

上記定理は類体論の成果の一つである。 類体論のおかげで、 アーベル拡大(とくに $\mbox{${\mathbb{Q}}$}$ の有限次代数拡大 $K$ のアーベル拡大)については、 上記定理の他にもいろいろなことがわかっている。 それでは、非アーベル拡大についてはどうかという疑問が当然生じるが、 それについては 現代でも活発に研究が行われているところである。