代数学III要約 No.11

代数関数体

No.10 で (2),3,4次方程式の解法について述べた。 これは $X^3+2 X^2+3 X+4 \in$   $\mbox{${\mathbb{Q}}$}$$[X]$ のような具体的な多項式の 根を求めると見ることもできるが、別の見方もできる。すなわち、 (2次方程式の場合で言えば)多項式

$$X^2- a X + b$$

の係数 $a,b$ を不定元(変数) とみて、そのような「普遍的な」2次多項式の根として

$$\frac{a \pm \sqrt{ a^2 -4 b} }{2}$$

を考え、その特殊な場合として一般の2次の多項式を扱うという具合である。

定義 11.1   体 $k$ 上の $n$-変数多項式環 $k[X_1,X_2,\dots, X_n]$ の商体(多項式の 分数の形で書けるもの全体のなす体)を $k(X_1,X_2,\dots, X_n)$ と書き、 体 $k$ 上の$n$-変数有理関数体と呼ぶ。

定義 11.2   体 $k$ 上の $n$-変数有理関数体 の有限次代数拡大を 代数関数体と呼ぶ。

例 11.3   体 $k$ 上の不定元 $a,b$ をとって2変数有理関数体 $K=k(a,b)$ を考える。 $K$ 上の多項式 $X^2-a X +b$ は $K$ 上既約であって、 その根の一つを $x_1$ とおくと、$L=K(x_1)$ は2変数代数関数体の例である。 $L$ は $K$ のガロア拡大で、 $\operatorname{Gal}(L/K) \cong C_2$ (2次の巡回群).

例 11.4   体 $k$ 上の不定元 $a,b,c$ をとって3変数有理関数体 $K=k(a,b,c)$ を考える。 $K$ 上の多項式 $X^3-a X^2 +b X + c$ は $K$ 上既約であって、 その根を $x_1,x_2,x_3$ とおくと、 $L=K(x_1,x_2,x_3)$ は2変数代数関数体の例である。 $L$ は $K$ のガロア拡大で、 $\operatorname{Gal}(L/K) \cong \mathfrak{S}_3$ (3個の元の対称群).

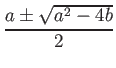
上の例は一般の次数の「普遍多項式」の場合にまで拡張できる。

命題 11.5   体 $k$ が $1$ の3乗根 $1,\omega, \omega^2$ を元として含むとする。 上の例の $K=k(a,b,c)$ と $L=K(x_1,x_2,x_3)$ を考えよう。

$$r_1= x_1 + \omega x_2 + \omega^2 x_3, \qquad r_2= x_1 + \omega^2 x_2 + \omega x_3$$

とおくと、

1. $M=K(r_1^3)$ は $K$ と $L$ の中間体であって、 $r_1^3,r_2^3\in M$, $L=M(r_1)$.
2. $M$ は $K$ の2次のガロア拡大で、 $\operatorname{Gal}(M/K)\cong C_2$.
3. $L$ は $M$ の3次のガロア拡大で $\operatorname{Gal}(L/M)\cong C_3$.

ガロア拡大で、そのガロア群が巡回群であるものを巡回拡大と呼ぶ。 上の命題は、「普遍的な」3次方程式の分解体が巡回拡大の繰り返しで 得られることを述べている。4次方程式についても同様のことができる。

有理関数体が出てきたついでに、次のことについても言及しておこう。

命題 11.6 (非分離拡大の例)   標数 $p$ の体 $k$ が与えられたとする。(例えば、 $k={\mathbb{F}}_p$.) このとき、$k$ 上の不定元 $a$ をひとつとって $K=k(a)$ を考える。 $X^p-a$ は $K$ 上既約であって、その根 $\alpha$ は $K$ 上分離的ではない。

問題 11.1   ${\mathbb{F}}_3$ 上の多項式 $X^3-1$ を因数分解せよ。

問題 11.2   上の命題 11.5 と同様の議論を4次方程式について 展開せよ。(少なくとも、$K$ と $L$ にあたるのものの中間体の 一つを見いだせ。)