代数学III要約 No.10
今日のテーマ:3次・4次の方程式の解法
3次方程式
を解こう。
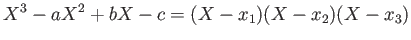 |
(★) |
を展開することにより、いわゆる根と係数の関係
が得られる。
ラグランジュの分解式
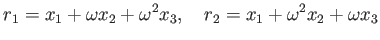 |
(R1) |
を考えてみよう。(ただし
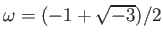 .)
これら自体は
.)
これら自体は
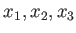 の対称式ではないが、
の対称式ではないが、
実際、
このことから、
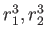 を二次方程式
を二次方程式
の二根として計算することができて、
あとはその3乗根として 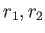 を計算できる。
を計算できる。
4次方程式の場合を考えよう。
根を
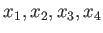 とおくと、
とおくと、
ラグランジュの分解式として、
をとる。
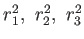 の基本対称式
の基本対称式
はそれぞれ
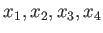 の対称式になっていることが分かり、したがって
の対称式になっていることが分かり、したがって 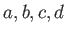 から計算できる。
すなわち、
から計算できる。
すなわち、
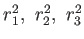 は
は
の三根であるから、前段のように巾根を用いて 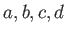 から計算できる。
あとはその平方根を計算すれば、
から計算できる。
あとはその平方根を計算すれば、
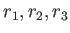 が計算されて、
一次方程式の根として
が計算されて、
一次方程式の根として
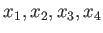 が計算されるという仕組である。
が計算されるという仕組である。
問題 10.1
3次方程式の解法において、
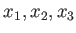
の置換(6つある)によって(R1)の分解式
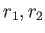
が
それぞれどのように変化するか、実際に書き下しなさい。
問題 10.2
4次方程式の解法で前問と同様のことを考えてみなさい。
[ガロア対応の証明]
体 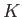 のガロア拡大
のガロア拡大 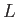 が与えられているとする。
が与えられているとする。
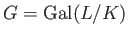 の部分群
の部分群 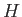 に対して、
に対して、
と定義する。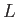 と
と 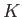 の中間体
の中間体 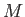 に対して、
に対して、
と定義する。この時、次のことが成り立つ。(単調減少性)
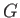 の任意の部分群
の任意の部分群 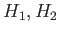 に対して、
に対して、
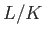 の任意の中間体
の任意の中間体 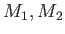 に対して、
に対して、
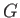 の任意の部分群
の任意の部分群 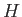 にたいして、
にたいして、
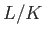 の任意の中間体
の任意の中間体 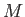 に対して、
に対して、
実は、上の (1)-(4) から、全く形式的な計算で次のことが成り立つことがわかる。
("3回=1回")
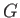 の任意の部分群
の任意の部分群 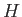 にたいして、
にたいして、
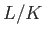 の任意の中間体
の任意の中間体 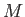 に対して、
に対して、
ガロア理論では、さらに次のことが分かる。(狭義単調減少性)
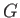 の任意の部分群
の任意の部分群 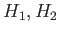 に対して、
に対して、
(補題9.2による。)
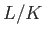 の任意の中間体
の任意の中間体 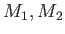 に対して、
に対して、
(命題8.5による。)
このことから、最後に次のことが分かる。
("2回=0回")
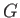 の任意の部分群
の任意の部分群 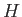 にたいして、
にたいして、
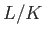 の任意の中間体
の任意の中間体 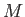 に対して、
に対して、
![]() を二次方程式
を二次方程式
![]() とおくと、
とおくと、
![]() のガロア拡大
のガロア拡大 ![]() が与えられているとする。
が与えられているとする。
![]() の部分群
の部分群 ![]() に対して、
に対して、