


Next: About this document ...
代数学 IA No.1要約
一学期の目標

 代数系, 特に, 群。
代数系, 特に, 群。
代数系とは、集合の上に演算を載せたものである。
載せる演算の種類によっていろいろなものができる。
| 演算 |
演算の記号 |
代数系 |
| 和, 差 |
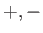
|
加群 |
| 積 |
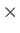
|
半群 |
| 積,商 |
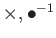
|
群 |
| 和,差,積 |
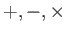
|
環 |
| 和,差,積,0
以外での商 |
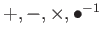
|
体 |
定義 1.1
集合
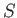
上の
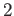
項演算とは、
写像
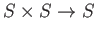
のことである。
○1項演算、3項演算、4項演算等も同様に定義される。
例えば、
例 1.3
-
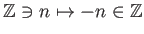 は
は
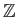 上の1項演算である。
上の1項演算である。
-
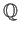
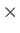
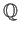
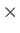
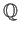
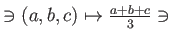
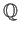 は
は
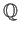 上の
上の 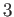 項演算である。
項演算である。
定義 1.4 (群の定義)
集合
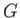
が群であるとは、
(群0)二項演算
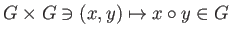 が定義されていて、
次の条件を満たすときに言う。
が定義されていて、
次の条件を満たすときに言う。
- (群1).
- その演算は結合法則を満たす。
- (群2).
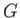 には単位元(普通
には単位元(普通 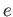 と書かれる)が存在する。すなわち、
ある
と書かれる)が存在する。すなわち、
ある 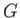 の元
の元 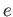 があって、
があって、
がなり立つ。
- (群3).
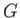 の各元には逆元がある。すなわち、
の各元には逆元がある。すなわち、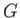 の任意の元
の任意の元 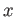 に対して、
に対して、
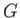 のある元
のある元 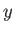 が存在して、
が存在して、
がなりたつ。
群の定義において、集合 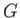 を決めただけではどんな演算を考えているのか
明確でないので、正確には、組
を決めただけではどんな演算を考えているのか
明確でないので、正確には、組 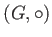 を群と呼ぶ。
を群と呼ぶ。
定義 1.7
演算が可換で、かつ
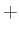
記号で書かれるような群のことを加法群
と呼ぶ。加法群は加群とも呼ばれる。
例 1.8
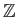
,
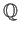
,
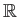
等はそれぞれ(通常の加法に関して)加法群である。
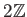
も加法群である。
加法群も群の一種に過ぎないことに注意。
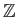 の加法群のことを
の加法群のことを
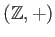 と書く。
と書く。
例 1.9
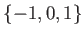
は(通常の加法に関して)群ではない。
問題
- (I).
-
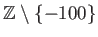 は加法に関して群をなすだろうか、
理由を挙げて述べなさい。
は加法に関して群をなすだろうか、
理由を挙げて述べなさい。
- (II).
-
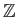 に、演算
に、演算 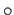 を
を
で定義する。このとき、
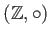 は群であるか、理由をつけて答えなさい。
は群であるか、理由をつけて答えなさい。
● http://www.math.kochi-u.ac.jp/docky/kogi にこのプリント
を提供する.



Next: About this document ...
2017-04-20
![]()
![]() 代数系, 特に, 群。
代数系, 特に, 群。
![]() が定義されていて、
次の条件を満たすときに言う。
が定義されていて、
次の条件を満たすときに言う。
![]() の加法群のことを
の加法群のことを
![]() と書く。
と書く。