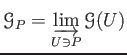
It should be noted at this stage that
LEMMA 06.17
Let
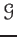 be a presheaf on a topological space
be a presheaf on a topological space 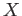 .
The natural map
.
The natural map

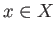 .
.
induces an isomorphism of stalk at each point
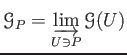
It should be noted at this stage that
induces an isomorphism of stalk at each point