be a ring homomorphism (which we always assume to be unital).
Then we have a associate map
defined by
The map
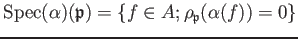
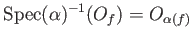
for any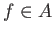 .
.
-
 is continuous.
is continuous.
be a ring homomorphism (which we always assume to be unital).
Then we have a associate map
defined by
The map
for any