今日のテーマ:行列式(2)
(もっと一般に、![]() の
の ![]() 列目が
列目が ![]() に等しいならば、
に等しいならば、
![]() .)
.)
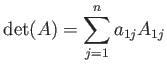
が成り立つ。
上の命題と同様にして、![]() 行目、
行目、![]() 行目,...
行目,... ![]() 行目に関する展開が
得られる。
行目に関する展開が
得られる。![]() を、「
を、「![]() の
の![]() 列目を
列目を ![]() の
の ![]() 列目に置き換えた行列」
に置き換えることにより、つぎの結果を得ることができる。
列目に置き換えた行列」
に置き換えることにより、つぎの結果を得ることができる。
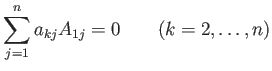
が成り立つ。
これもまた、![]() 行目だけについて特別に言えることではなく、結局次のことが言える:
行目だけについて特別に言えることではなく、結局次のことが言える:
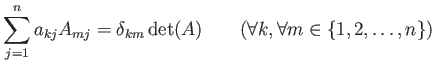
が成り立つ。
この式は次のことを意味している: