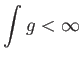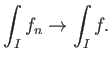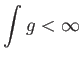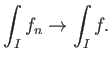Next: About this document ...
微分積分学基礎 No.13要約
今日のテーマ:積分記号下の極限,微分
次の定理はルベーグ積分で語られるべきだが、ここで結果だけ引用する。
ルベーグ積分を本格的に学ぶ時間がない場合には、覚えておいても良いと思う。
定理 13.1 (優収束定理)
![$ I=[a,b]$](img1.png)
上の関数
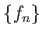
と
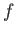
があって、
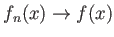
(各点収束) であるとする。
いま、
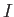
上の正値関数
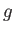
が
を満たして、
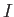
の各点で
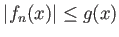
であったとするならば、
この定理自体は、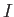 が無限区間でも成り立つ。
が無限区間でも成り立つ。
優関数の存在が大事であって、それなしではうまく行かない。
2017-07-14