


Next: About this document ...
微分積分学基礎 No.2要約
今日のテーマ:数列
定義 2.1
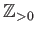
上の関数を数列という。数列のことを
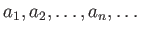
と書いたり、
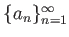
と書いたりする。
単に数列と言ったときには、有限数列は考えない。
他方で、「(添字が)0
から始まる数列」なども場合によっては考えることがあるが、
それについては臨機応変に。
◎有界
定義 2.2
-
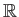 の部分集合
の部分集合 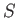 が有界であるとは、
ある実数
が有界であるとは、
ある実数 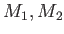 があって、どのような
があって、どのような 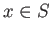 に対しても
に対しても
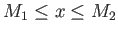 を満たすときに言う。
を満たすときに言う。
- 実数列
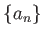 が有界であるとは、
それを
が有界であるとは、
それを
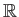 の部分集合と見て有界であるときに言う。
の部分集合と見て有界であるときに言う。
- 集合
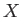 上の関数
上の関数 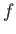 が有界であるとは、値集合
が有界であるとは、値集合
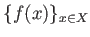 が有界であるときにいう。
が有界であるときにいう。
(2) は (3)の特別の場合とも見ることができる。(3)については次回以降に解説する。
◎極限
定義 2.3
数列
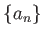
は、ある実数
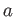
にたいして、
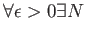
such that
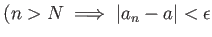
をみたすとき、
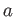
に
収束する という。
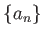
が
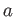
に収束するとき、 その収束する先
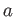
は一つに定まる。そこで
この値のことを
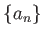
の
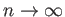
のときの
極限とよび、
と表す。
命題 2.4
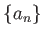
と
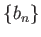
とが収束すると仮定する。このとき、
- さらに
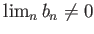 を仮定すると、
有限個の例外を除いて
を仮定すると、
有限個の例外を除いて 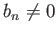 で、
で、
2017-04-20