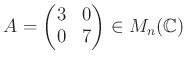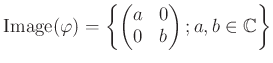Next: About this document ...
пњљпњљпњљпњљЎ±йљђ IB пњљпњљпњљпњљ No.6

пњљпњљпњљпњљ 6.2 (пњљпњљпњљпњљпњљпњљ1)
пњљпњљпњљпњљ
пњљЎ§ќіƒљпњљ∆±пњљпњљ
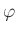
пњљпњљпњљпњљпњљ√§пњљпњљ»§пњљпњљл°£
-
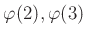 пњљпњљпњљпњљи°£
пњљпњљпњљпњљи°£
- «§пњљ’§пњљ
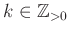 пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
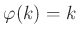 пњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
-
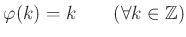 пњљтЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљтЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 6.4
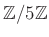
пњљпњљпњљпњљ
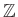
пњљЎ§ќіƒљпњљ∆±пњљпњљпњљпњљ
¬Єпњљя§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ¬Єпњљя§пњљпњљпњљпњљпњљЋ§пњљпњљпњљпњљ∆µу§≤°пњљ
¬Єпњљя§пњљпњљ §пњљпњљпњљпњљѕ§пњљпњљпњљпњљпњљЌ≥пњљпњљќ§ў§и°£
пњљпњљпњљпњљ 6.5
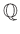
пњљпњљпњљпњљ
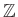
пњљЎ§ќіƒљпњљ∆±пњљпњљпњљпњљ
¬Єпњљя§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ¬Єпњљя§пњљпњљпњљпњљпњљЋ§пњљпњљпњљпњљ∆µу§≤°пњљ
¬Єпњљя§пњљпњљ §пњљпњљпњљпњљѕ§пњљпњљпњљпњљпњљЌ≥пњљпњљќ§ў§и°£
пњљпњљпњљпњљ 6.6
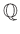
пњљпњљпњљпњљ
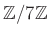
пњљЎ§ќіƒљпњљ∆±пњљпњљпњљпњљ
¬Єпњљя§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ¬Єпњљя§пњљпњљпњљпњљпњљЋ§пњљпњљпњљпњљ∆µу§≤°пњљ
¬Єпњљя§пњљпњљ §пњљпњљпњљпњљѕ§пњљпњљпњљпњљпњљЌ≥пњљпњљќ§ў§и°£
пњљпњљпњљпњљ 6.7
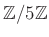
пњљпњљпњљпњљ
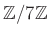
пњљЎ§ќіƒљпњљ∆±пњљпњљпњљпњљ
¬Єпњљя§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ¬Єпњљя§пњљпњљпњљпњљпњљЋ§пњљпњљпњљпњљ∆µу§≤°пњљ
¬Єпњљя§пњљпњљ §пњљпњљпњљпњљѕ§пњљпњљпњљпњљпњљЌ≥пњљпњљќ§ў§и°£
пњљпњљпњљпњљ 6.9
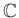
пњљпњљпњљпњљ
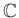
пњљЎ§ќљпњљ∆±пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ(пњљ Њпњљ)пњљу§≤§ §пњљпњљпњљпњљпњљ
(пњљпњљƒ§ѕ§пњљпњљ §пњљпњљ√±пњљЋЄпњљпњљƒ§пњљпњљл§ђпњљпњљпњљпњљпњљƒ§пњљпњљу§≤§пњљќ§пњљƒґпњљпњљпњљпњљ«§пњљпњљл°£
槮ќ§пњљћµпњљпњљ«§пњљпњљл°£)
пњљ ≤пњљпњљпњљпњљќ±йљђпњљ«§ѕ°пњљпњљ»§пњљпњљпњљпњљ«§пњљ §пњљпњљпњљ
![$ [?]_n$](img32.png) пњљпњљ
пњљпњљ 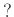 пњљпњљ
пњљпњљ
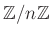 пњљ«§ќ•пњљпњљй•єпњљпњљ…љпњљпњљпњљпњљпњљ»§пњљпњљпњљпњљл°£
ЄћЃпњљ«§п§Ђпњљпњљ»ї„§пњљпњљќ§«°пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљс§Ђ§ §пњљпњљпњљпњљпњљпњљпњљпњљ’§пњљпњљ∆§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљ«§ќ•пњљпњљй•єпњљпњљ…љпњљпњљпњљпњљпњљ»§пњљпњљпњљпњљл°£
ЄћЃпњљ«§п§Ђпњљпњљ»ї„§пњљпњљќ§«°пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљс§Ђ§ §пњљпњљпњљпњљпњљпњљпњљпњљ’§пњљпњљ∆§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 6.10
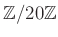
пњљпњљпњљпњљ
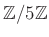
пњљЎ§ќЉпњљпњљпњљ
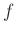
пњљпњљ
пњљпњљпњљпњљпњљл°£
пњљпњљпњљќ§»§пњљпњљпњљ
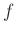
пњљѕ§пњљпњљё§пњљпњљпњљпњљпњљпњљпњљпњљ∆§пњљпњљ∆°пњљпњљƒљпњљ∆±пњљпњљпњљ«§пњљпњљпњљ
пњљпњљпњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 6.11
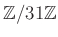
пњљпњљпњљпњљ
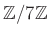
пњљЎ§ќЉпњљпњљпњљ
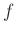
пњљпњљ
пњљпњљпњљпњљб§њпњљпњљпњљпњљпњљпњљ
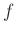
пњљѕ§пњљпњљё§пњљпњљпњљпњљпњљпњљпњљпњљ∆§пњљпњљ∆°пњљпњљƒљпњљ∆±пњљпњљпњљ«§пњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЌ≥пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 6.12
пњљпњљ
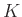
пњљпњљпњљпњљ пњљпњљ
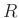
пњљЎ§ќљпњљ∆±пњљпњљпњљпњљпњљпњљпњљпњљ
…ђпњљпњљ√±пњљЌ§«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 6.13
пњљƒљпњљ∆±пњљпњљпњљпњљпњљпњљ
![$ f:{\mbox{${\mathbb{Z}}$}}/18{\mbox{${\mathbb{Z}}$}}\ni [x]_{18}\mapsto [x]_6 \in {\mbox{${\mathbb{Z}}$}}/6{\mbox{${\mathbb{Z}}$}}$](img41.png)
пњљпњљЌ§пњљпњљл°£
пњљпњљпњљпњљ№§пњљ
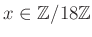
(18пњљпњљ), пњљпњљпњљпњљ№§пњљ
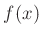
пњљпњљпњљ¬§пњљпњљпњљи§¶пњљпњљ…љпњљпњљпњљк°Ґ
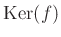
,
![$ f^{-1}([1]_6)$](img45.png)
,
![$ f^{-1}([2]_6)$](img46.png)
пњљт§љ§м§Њпњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 6.14
пњљƒљпњљ∆±пњљпњљпњљпњљпњљпњљ
![$ f:{\mbox{${\mathbb{Z}}$}}/20{\mbox{${\mathbb{Z}}$}}\ni [x]_{20} \mapsto [x]_{4}\in {\mbox{${\mathbb{Z}}$}}/4{\mbox{${\mathbb{Z}}$}}$](img47.png)
пњљпњљЌ§пњљпњљл°£
пњљпњљпњљпњљ№§пњљ
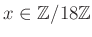
(18пњљпњљ), пњљпњљпњљпњљ№§пњљ
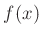
пњљпњљпњљ¬§пњљпњљпњљи§¶пњљпњљ…љпњљпњљпњљк°Ґ
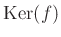
,
![$ f^{-1}([1]_6)$](img45.png)
,
![$ f^{-1}([2]_6)$](img46.png)
пњљт§љ§м§Њпњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 6.15
пњљпњљпњљпњљ
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљл°£
пњљпњљпњљќ§»§пњљпњљпњљ
-
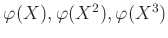 пњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
-
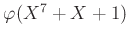 пњљпњљпњљ»§пњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљ»§пњљ §пњљпњљпњљпњљпњљ
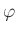 пњљѕіƒљпњљ∆±пњљпњљпњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљѕіƒљпњљ∆±пњљпњљпњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
-
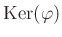 пњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
пњљ«§пњљпњљл§≥пњљ»§пњљпњљпњљпњљпњљпњљпњљ §пњљпњљпњљпњљпњљ



Next: About this document ...
2016-11-04
![]()
![]() пњљпњљ
пњљпњљ ![]() пњљпњљ
пњљпњљ
![]() пњљ«§ќ•пњљпњљй•єпњљпњљ…љпњљпњљпњљпњљпњљ»§пњљпњљпњљпњљл°£
ЄћЃпњљ«§п§Ђпњљпњљ»ї„§пњљпњљќ§«°пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљс§Ђ§ §пњљпњљпњљпњљпњљпњљпњљпњљ’§пњљпњљ∆§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљ«§ќ•пњљпњљй•єпњљпњљ…љпњљпњљпњљпњљпњљ»§пњљпњљпњљпњљл°£
ЄћЃпњљ«§п§Ђпњљпњљ»ї„§пњљпњљќ§«°пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљс§Ђ§ §пњљпњљпњљпњљпњљпњљпњљпњљ’§пњљпњљ∆§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ