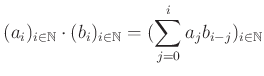Next: About this document ...
����ر齬 IB ���� No.2

����
���줫��ϡ��Ȥ��ˤ��Ȥ��ʤ��¤ꡢñ�̸����ĴĤΤߤ����ִġפȤ����С�
ñ�̸�����ĴĤȲ�ᤷ�Ƥ�������������(ñ�̸���¸�ߤ��Ȥ��˽��פʻ��ˤϡ�
������Ȥ�롣)���������Ѥ��Ĵ��Ǥ���ȤϤޤ����ꤷ�ʤ���
���� 2.1
ñ�̸�
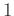
����Ĵ�
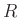
�θ�
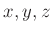
�ˤ������ơ�
| |
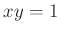 (���ʤ�� (���ʤ�� 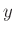 ��
�� 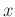 �α��ո��Ǥ��롣)
�α��ո��Ǥ��롣) |
|
| |
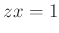 (���ʤ�� (���ʤ�� 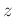 ��
�� 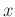 �κ��ո��Ǥ��롣)
�κ��ո��Ǥ��롣) |
|
������Ω�ĤȤ���
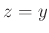
�Ǥ��äơ�
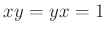
(���ʤ�� $y(=z)$ �� $x$ �εո��Ǥ���)
������Ω�Ĥ��Ȥ��ʤ�����
��� 2.1
ñ�̸���¸�ߤ����
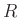
�ˤ����ơ�
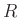
�Τʤ��ǵո���¸�ߤ���褦�ʸ��Τ��Ȥ�
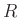
��
�ĵո��Ȥ���
ñ�������뤤��
ñ���Ȥ����ޤ���
��������
(1)���ܼ�Ū��ʬ�Ǥ��ꡢ(2) ����Ƭ�ǽҤ٤����դ˱褦�����
����Ū���Ǥ��롣��������(2)��̤����Ƥ��ޤ��������ϸ������夫�ʤ��ä�
���ˤʤ�Τ�ñ�̸��Τʤ��Ĥ���(���⤷����Ф��λ�)�ˤ����դ�ɬ�פǤ��롣
���� 2.3
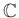
����ʬ��
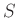
����
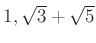
�Ȥ��ƻ��äƤ���Ȥ��ޤ���
�����
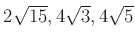
��
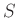
�θ��Ǥ��뤳�Ȥ��ʤ�����
���� 2.4
ͭ����������
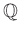
����ʬ�ĤȤ��ƴޤ�褦��
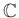
����ʬ��
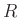
(�Ĥޤꡢ
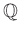
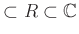
)
��
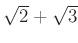
�Ȥ��ƴޤ�Ȥ���
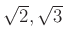
��
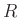
�θ��Ǥ��뤳�Ȥ��ʤ�����
���� 2.5
ͭ����������
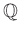
����ʬ�ĤȤ��ƴޤ�褦��
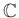
����ʬ��
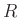
��
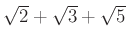
�Ȥ��ƴޤ�Ȥ���
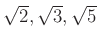
��
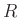
�θ��Ǥ��뤳�Ȥ��ʤ�����
���� 2.6
ͭ����������
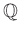
����ʬ�ĤȤ��ƴޤ�褦��
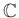
����ʬ��
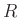
��
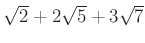
�Ȥ��ƴޤ�Ȥ���
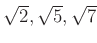
��
�θ��Ǥ��뤳�Ȥ��ʤ�����
���� 2.7
ͭ����������
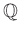
����ʬ�ĤȤ��ƴޤ�褦��
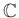
����ʬ��
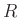
�ˤĤ��ơ�������Ĥξ���Ʊ�ͤǤ��뤳�Ȥ�
�����ʤ�����
-
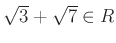 .
.
-
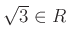 ����
����
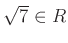 .
.
���� 2.8
����ǡ�
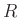
��
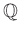
����ʬ�ĤȤ��ƴޤࡢ�Ȥ�������
�����Ƥ�Ʊ�ͤΤ��Ȥ����������������
�������ʤ���������ְ�äƤ���ʤ�ȿ���
�����ʤ�����
���� 2.10 (��1)
�Ȥ��������ΤȤ���
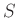 ��
��
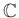 ����ʬ�ĤǤ������������
����ʬ�ĤǤ������������
-
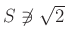 �ᤷ�ʤ�����
�ᤷ�ʤ�����
-
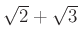 �Ȥ��ƴޤ�褦��
�Ȥ��ƴޤ�褦��
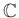 ����ʬ��
����ʬ�� 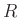 ��
���ʤ餺
��
���ʤ餺 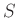 ����ʬ����Ȥ��ƴޤळ�Ȥ��ʤ�����
����ʬ����Ȥ��ƴޤळ�Ȥ��ʤ�����
���� 2.11 (��1)
-
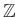 �βĵո������Ƶ��衣
�βĵո������Ƶ��衣
- ���̤δ�
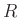 �ˤĤ��ơ�
�ˤĤ��ơ� 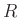 �βĵո������Τ�
����ʤ����Ȥ�������衣
�βĵո������Τ�
����ʤ����Ȥ�������衣
��������Ͼ����ѡ����äƺ٤��������Ϥ��ʤ���
���Ȼפ���ΤϾܺ٤ϼ�ʬ�ǹͤ��뤳�ȡ�
�ʲ���
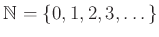 �Ȥ���������Ѥ��롣
�Ȥ���������Ѥ��롣
���� 2.12 (��1)
��
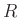
��Ϳ�����Ƥ���Ȥ��롣
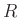
����������
�ˡ���ʬ���Ȥ��¤��¤��������
�Ѥ�
���������Ȥ���
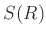 �Ϥ����¤��ѤˤĤ��ƴĤ�ʤ����Ȥᤷ�ʤ�����
�Ϥ����¤��ѤˤĤ��ƴĤ�ʤ����Ȥᤷ�ʤ�����
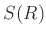 �ΤΤΤ�����ͭ�¿���Ǥ����Τ�
(���ʤ��������
�ΤΤΤ�����ͭ�¿���Ǥ����Τ�
(���ʤ�������� 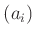 �Ǥ��äơ�
��
�Ǥ��äơ�
��
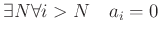 ��
�����������)
����
��
�����������)
���Τ� 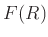 �Ƚȡ������
�Ƚȡ������ 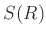 ����ʬ�Ĥ�ʤ����Ȥᤷ�ʤ�����
����ʬ�Ĥ�ʤ����Ȥᤷ�ʤ�����
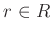 ���Ф��ơ�
���Ф��ơ�
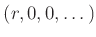 ��
�� 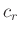 ��
���Ȥˤ��롣
��
���Ȥˤ��롣
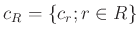 ��
�� 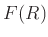 ��
��ʬ�ĤǤ��뤳�Ȥ��ʤ�����
��
��ʬ�ĤǤ��뤳�Ȥ��ʤ�����
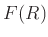 �ϡ�
�ϡ� 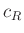 ��
��
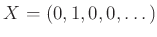 ����������뤳�Ȥ�
�����ʤ�����
����������뤳�Ȥ�
�����ʤ�����



Next: About this document ...
2016-10-14
![]()
![]() �Ȥ���������Ѥ��롣
�Ȥ���������Ѥ��롣