


Next: About this document ...
論理と集合要約 No.8
写像を理解するときに、「ホテルヒルベルト」のような解釈もできるのでした。
この解釈では、全射は、「空き室がないこと」に対応し、
単射は、「各部屋個室」(単射でないことは、
相部屋が生じること)に対応するのでした。
全射や単射の存在は、始集合と終集合の元の多さと関係しているのでした。
&dotfill#dotfill;
第8回目の主題 : 写像、合成写像
◎写像の合成
定義 8.1
写像
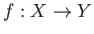
と
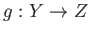
が与えられているとする。
このとき、
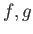
の
合成写像
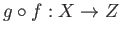
を
で定義する。
次の命題は簡単ではあるが有用である。実用上はこのような命題があることだけ
記憶しておいて、その都度頭の中で確かめるのがいいだろう。
定義 8.3
集合
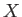
に対して、写像
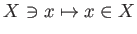
を
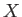
の
恒等写像といい、
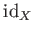
で表す。
上の命題も、
 以外はその都度確認すれば良い。
以外はその都度確認すれば良い。
 は特に重要である。
は特に重要である。
問題 8.2
![$ X={\mathbb{C}}[t] $](img24.png)
(複素数係数の
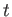
を変数とする多項式の全体のなす集合),
![$ Y={\mathbb{C}}[t]$](img26.png)
とおく。
写像
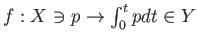
と
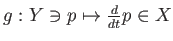
にたいして、
-
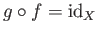 であることを示しなさい。
であることを示しなさい。
-
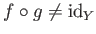 であることを示しなさい。
であることを示しなさい。
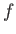 ,
, 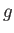 はそれぞれ全射、単射、全単射だろうか。
はそれぞれ全射、単射、全単射だろうか。
Yoshifumi Tsuchimoto
2016-06-08