第2回目の主題 :
![]()
◎ 論理(続き)
論理においては、命題が大事であって、それらは基本的な命題
から, and, or, not, ![]() ,
, ![]() を用いて作れるのでした。
を用いて作れるのでした。
![]() は、「どんな
は、「どんな ![]() にたいしても
にたいしても ![]() が成立する。」ということ、
が成立する。」ということ、
![]() は、「ある
は、「ある ![]() にたいして
にたいして ![]() が成立する。」
(どれかひとつの
が成立する。」
(どれかひとつの ![]() について
について ![]() が成立する。)
という意味でした。
が成立する。)
という意味でした。
&dotfill#dotfill;
「![]() ならば
ならば ![]() 」は、
」は、![]() が成り立つときには、
が成り立つときには、![]() が成り立つことを
主張している。では
が成り立つことを
主張している。では ![]() が成り立たないときにはどうだろうか。
日常生活では場合に応じて次の二つの意味に用いている。
が成り立たないときにはどうだろうか。
日常生活では場合に応じて次の二つの意味に用いている。
「![]() または
または ![]() 」(
」( ![]() or
or ![]() )についても
これは
)についても
これは ![]() と
と ![]() のどちらかが正しいという主張であるが、
日常生活では場合に応じて次の二つの意味に用いている。
のどちらかが正しいという主張であるが、
日常生活では場合に応じて次の二つの意味に用いている。
極論すれば、
論理とは、ある仮定 ![]() をおいたときに、正しい推論規則を用いて
結論
をおいたときに、正しい推論規則を用いて
結論 ![]() を導き出すことにより、
を導き出すことにより、
![]() を証明することに他ならない。
を証明することに他ならない。
![]() と
と ![]() の真理値がいつでも一致するとき、
の真理値がいつでも一致するとき、 ![]() と
と ![]() とは
同値であるといい、
とは
同値であるといい、
![]() と書く。
これは 「(
と書く。
これは 「(
![]() ) かつ (
) かつ (
![]() )」 と同じことである。
)」 と同じことである。
日常用いているいくつかの基本的な推論規則も、真理表を用いて直ちに 導きだすことができる。例えば次のような具合である。
集合 ![]() にたいして、
にたいして、![]() が
が ![]() に属するとき、
に属するとき、![]() は
は ![]() の元(要素)
であるといい、
の元(要素)
であるといい、 ![]() とか、
とか、 ![]() と
書き、そうでないとき
と
書き、そうでないとき ![]() とか
とか
![]() と書く。
と書く。
あとの、「部分集合として含まれる」との区別を強調するため、
![]() のことを
「
のことを
「 ![]() は
は ![]() に元として含まれる。」という読み方をすることもある。
に元として含まれる。」という読み方をすることもある。
集合は、中カッコの中に集めるものを言葉で、あるいはリストアップして 書きだすことにより表現できる。下の例を見よ。
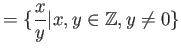 .
.
例えば上の(3)のように、![]() の式
の式 ![]() と、
と、 ![]() を
変数とする命題
を
変数とする命題 ![]() にたいして、
にたいして、
なる集合を考えることができる。これは
微分積分学で使う「区間」についても書いておこう。
二つの集合 ![]() が等しいことを示すには、
「
が等しいことを示すには、
「![]() 」 と 「
」 と 「![]() 」 とが同値であることを証明するのが常道である。
」 とが同値であることを証明するのが常道である。
を示しなさい。
をみたすとき、
(
この定義と上で述べたことを用いると、
であることが分かる。
次の問題も部分集合の定義に戻って考えれば良い。
をそれぞれ
![]() は
は ![]() キャップ
キャップ ![]() とか、
とか、![]() インターセクション
インターセクション ![]() と読む。「
と読む。「![]() かつ
かつ ![]() 」 と読む人もいるが紛らわしいから
やめておいたほうが良い。同様に、
」 と読む人もいるが紛らわしいから
やめておいたほうが良い。同様に、
![]() は
は ![]() カップ
カップ ![]() とか、
とか、![]() ユニオン
ユニオン ![]() と読む。
と読む。
次のことは対応する論理の結果からすぐに分かる。