


Next: About this document ...
代数学II要約 No.7
第7回目の主題 :
補題 7.1
PID
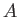
上の加群
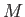
の元の組
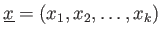
が与えられているとする。さらに、
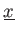
の関係式
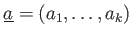
および
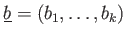
が与えられているとする。
つまり、2つの関係式
が与えるとする。内積の記法の真似をして、このことを
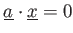
,
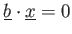
と表記しよう。
このとき、ある
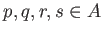
が存在して、次のことが成り立つ。
-
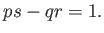
-
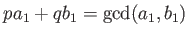 .
.
-
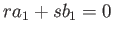 .
.
そこで、
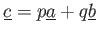
,
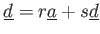
とおくと、
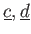
は
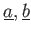
と同等の
関係式(つまり、互いに他から導かれる関係式)で、
をみたす。
この補題を用いると、前回の定理よりすこし強い主張をすることができる。
定理 7.3
可換 PID
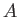
上の有限生成加群
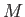
が与えられているとする。
このとき、
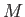
の生成系
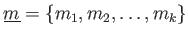
にたいして、
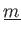
を(変換1),(変換2),(変換3)を有限回繰り返すことにより、
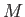
の新しい生成系
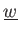
であって、
(巡回加群の直和)となるものが存在する。
さらに、上の同型は
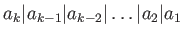 となるように取れる。
となるように取れる。
系 7.4 (有限生成アーベル群の基本定理)
任意の有限生成アーベル群
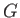
は巡回群の有限個の直和である。
もっと詳しくは、
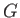
は
(
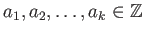
)
という加群とアーベル群として同型である。
系7.4の応用として、次の定理を挙げておく。
定理 7.5
体
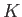
の乗法群
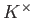
の有限部分群は常に巡回群である。
とくに、有限体の乗法群はかならず巡回群である。
Yoshifumi Tsuchimoto
2016-06-02
![]()
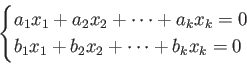
![]() となるように取れる。
となるように取れる。