Next: About this document ...
代数学II要約 No.5
第5回目の主題 : 有限生成加群と自由加群の間の準同型
,
PID 上の有限生成加群の構造(1)
◎有限生成加群 (再掲)
定義 5.1
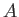
-加群
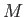
が有限個の元で生成されるとき、
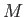
を
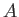
上の
有限生成加群と呼ぶ。
例 5.2
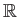
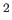
は 有限生成
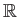
-加群だが、
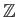
-加群としては有限生成ではない。
補題 5.3
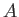
-加群
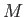
が有限個の元
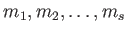
で生成されるとき、
- 写像
は 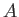 -加群の全射準同型である。
-加群の全射準同型である。
-
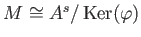 .
.
**
一般に、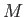 の
の 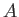 -加群としての生成元
-加群としての生成元
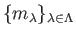 を
とれば、全射
を
とれば、全射 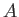 -準同型
-準同型
が定義されて、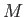 は自由加群の剰余加群として表現されることが分かる。
**
は自由加群の剰余加群として表現されることが分かる。
**
自由加群から一般の加群への準同型は次のように「生成元の行き先」で定まる。
うえのことは、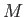 が適当な有限性の条件を満足すれば(つまり、有限表示を持てば)、
が適当な有限性の条件を満足すれば(つまり、有限表示を持てば)、
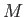 は
上のような準同型の余核として得られることを示している。
は
上のような準同型の余核として得られることを示している。
命題 5.6
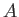
は可換環であるとする。このとき、
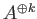
から
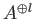
への任意の
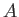
-準同型
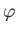
は、
と書ける。
PID 上の有限生成加群の構造(1)
次のことをこの講義からしばらくの間の目標にしよう。
定理 5.7
PID
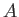
上の有限生成加群は必ず
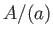
の形の加群の直和である。
言葉の確認から:
可換環 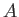 は、0
以外に零因子を持たないとき整域と呼ばれるのでした。
は、0
以外に零因子を持たないとき整域と呼ばれるのでした。
定義 5.8
整域
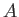
が
PID (principal ideal domain, 主イデアル整域) であるとは、
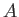
の任意のイデアルがひとつの元で生成されるときにいう。
「余りを許した割り算」が必ずできるような整域のことを
ユークリッド整域と呼ぶのでした。
次の定理は代数IB で学習済みのことと思います。
定理 5.9
ユークリッド整域は必ずPIDである。
定理 5.10
PID はかならず
UFD である。すなわち、素因数分解の一意性が成り立つ。
これらの諸定理から、次のことがすぐに分かる。
命題 5.11
PID
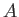
上の加群が、ひとつの元で生成されるなら、
それは
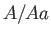
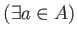
の形の加群と同型である。
補題 5.12
PID
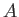
上の加群
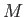
が2つの元
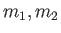
で生成されているとし、
なる関係式が成り立っていたとする。このとき、
次のような
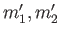 が存在する。
が存在する。
-
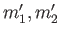 は
は 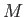 の生成元である。
の生成元である。
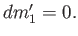 (ただし
(ただし 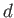 は
は 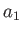 と
と 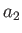 の最大公約元。)
の最大公約元。)
命題 5.13
可換 PID
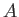
の元
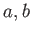
に対して、イデアル
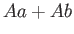
は
ある単項イデアル
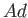
と等しい。このとき、ある
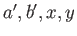
が存在して、
次の二式が成り立つ。
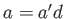 ,
, 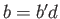 .
.
-
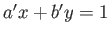 .
.
とくに、
は
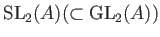
の元である。
命題 5.14
可換 PID
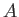
のイデアルの増加列
は必ず有限で止まる。すなわち、ある
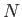
があって、
が成り立つ。



Next: About this document ...
Yoshifumi Tsuchimoto
2016-06-02
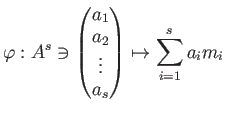
![]() の
の ![]() -加群としての生成元
-加群としての生成元
![]() を
とれば、全射
を
とれば、全射 ![]() -準同型
-準同型
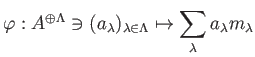
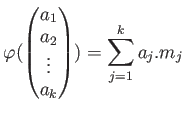
![]() が適当な有限性の条件を満足すれば(つまり、有限表示を持てば)、
が適当な有限性の条件を満足すれば(つまり、有限表示を持てば)、
![]() は
上のような準同型の余核として得られることを示している。
は
上のような準同型の余核として得られることを示している。
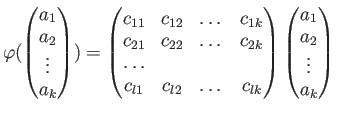
![]() は、0
以外に零因子を持たないとき整域と呼ばれるのでした。
は、0
以外に零因子を持たないとき整域と呼ばれるのでした。
![]() が存在する。
が存在する。