


Next: About this document ...
代数学II要約 No.2
第2回目の主題 : 環の上の加群の定義(2)
環と、その上の加群について、前回は「フォーマルな」定義を述べた。
実際には、次のことをわきまえていればそれほど間違えることはない。
- 環
 とは、その中で足し算、引き算、かけ算ができるような集合である。
とは、その中で足し算、引き算、かけ算ができるような集合である。
 -加群
-加群 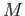 とは、その中で足し算、引き算、および
とは、その中で足し算、引き算、および
 の元による作用(「スカラー倍」)ができるような集合である。
の元による作用(「スカラー倍」)ができるような集合である。
例 2.1
環

が与えられたとき、正の整数
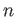
にたいし、

の元を
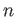
個縦に並べた「ベクトル」の全体
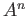
は

-加群とみなせる。
具体的には、
- 和
- 作用(スカラー倍)
上の例で 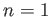 のときを考えれば、
のときを考えれば、 自身も
自身も  -加群とみなせることが
わかる。
-加群とみなせることが
わかる。
定義 2.2
上の
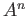
のことを

上の(階数
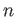
の)
自由加群と呼ぶ。
「 加群
加群 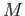 」を思いうかかべるとき、
はじめはベクトル空間をイメージしても
良いだろう。
ただし、つぎのことがベクトル空間とは決定的に異なる。
」を思いうかかべるとき、
はじめはベクトル空間をイメージしても
良いだろう。
ただし、つぎのことがベクトル空間とは決定的に異なる。
- 環
 の積は可換とは限らない。
(これは
の積は可換とは限らない。
(これは  が可換環であるような状況ならば回避できる。)
が可換環であるような状況ならば回避できる。)
- 環
 の元で割れるとは限らない。
の元で割れるとは限らない。
というわけで、加群を学ぶときには、ベクトル空間の性質を思い出しつつ、
加群の場合の違いを意識しながら学ぶと良いだろう。
次の定義はベクトル空間の間の線型写像の類似と考えて良い。
定義 2.4
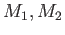
が

-加群のとき、写像
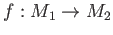
が
 -準同型
-準同型(
 -加群としての準同型)
-加群としての準同型))であるとは、
つぎの条件が満足されるときに言う。
- Hom1.
-
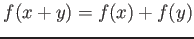
- Hom2.
-
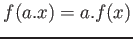
もっと一般に、
定義 2.8
環

にたいして、

自身を

-加群とみなしたものの部分加群
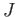
を

の
左イデアルと呼ぶ。別の言い方をすると、

の左イデアル
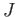
とは、

の部分集合であって、次の条件を満たすもののことである。
- LI1.
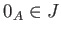 .
.
- LI2.
-
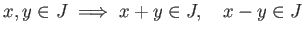 .
.
- LI3.
-
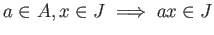 .
.
 が可換環のときには、左イデアルとイデアルは同じものである。
が可換環のときには、左イデアルとイデアルは同じものである。
定義 2.9

-加群
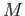
とその

-部分加群
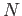
が与えられているとする。
このとき
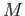
の
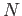
による商加群
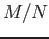
は自然に

-加群の構造をもつ。
問題 2.1
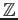
-加群
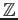
の
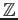
-部分加群
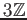
による剰余加群
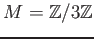
を考える。
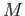
の各元
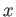
は 「
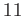
で割る」ことが
できること、すなわち、
を示しなさい。



Next: About this document ...
Yoshifumi Tsuchimoto
2016-06-02
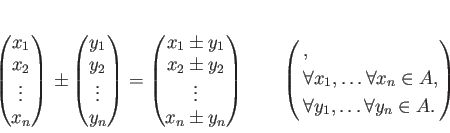
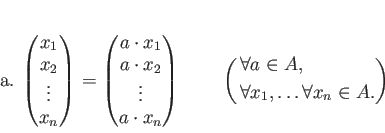
![]() 加群
加群 ![]() 」を思いうかかべるとき、
はじめはベクトル空間をイメージしても
良いだろう。
ただし、つぎのことがベクトル空間とは決定的に異なる。
」を思いうかかべるとき、
はじめはベクトル空間をイメージしても
良いだろう。
ただし、つぎのことがベクトル空間とは決定的に異なる。