$\mathbb{Z}_p$ , $\mathbb{Q}_p$ , and the ring of Witt vectors

No.12:

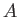
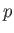
DEFINITION 12.1   Let $A$ be a ring of characteristic $p$ . We call the ring

$$\mathcal W^{(p)}_n(A)= \mathcal W^{(p)}(A)/V_p^n (\mathcal W^{(p)}(A))$$

the ring of Witt vectors of length 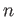$n$ . Its elements are called Witt vectors of lenth 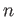$n$ .

Note that

$$\mathcal W^{(p)}(A)/V_p^n (\mathcal W^{(p)}(A))$$

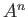
may be considered as a set $A^n$ with an unusual ring structure.

PROPOSITION 12.2  

$$\mathbb{Z}_p \cong \mathcal W^{(p)}(\mathbb{F}_p).$$

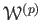
PROOF.. Since $\mathcal W^{(p)}$ is a unital commutative ring, there naturally exists a natural ring homomorphism

$$\iota:\mathbb{Z}\to \mathcal W^{(p)}(\mathbb{F}_p).$$

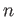
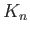
Let us first fix a positive integer $n$ and examine the kernel $K_n$ of a map

$$\pi_n\circ \iota: \mathbb{Z} \to \mathcal W^{(p)}(\mathbb{F}_p)/V_p^n (\mathcal W^{(p)}(\mathbb{F}_p))$$

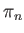
where $\pi_n$ is the natural projection. Since

$$\char93 \mathcal W^{(p)}(\mathbb{F}_p)/V_p^n (\mathcal W^{(p)}(\mathbb{F}_p)) =\char93 (\mathbb{F}_p^n)=p^n,$$

we have

$$\char93 (\mathbb{Z}/K_n) \vert p^n.$$

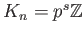
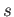
In other words, $K_n=p^{s} \mathbb{Z}$ for some integer $s$ . On the other hand, we have

$$\pi_n \circ\iota(p^s)=(1-T)^{p^s}=(1-T^{p^s})$$

thus

$$\pi_n \circ\iota(p^s)\in K_n \iff s\geq n.$$

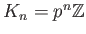
This implies that $K_n=p^n \mathbb{Z}$ and therefore we have an inclusion

$$\mathbb{Z}/p^n \mathbb{Z}\hookrightarrow W^{(p)}_n(\mathbb{F}_p)$$

which turns to be a bijection ( $\because \char93 (\mathbb{Z}/p^n \mathbb{Z})=\char93 (\mathcal W^{(p)}_n(\mathbb{F}_p))$ ).

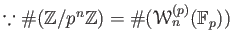
We then take a projective limit of the both hand sides and obtain the resired isomorphism.

$\qedsymbol$