


Next: About this document ...
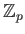 ,
,
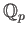 , and the ring of Witt vectors
, and the ring of Witt vectors
No.10:
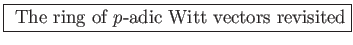
LEMMA 10.1
Let 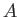 be a commutative ring. Then:
be a commutative ring. Then:
- For any
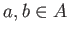 , we have
, we have
- If
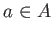 satisfies
satisfies 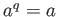 for some positive integer
for some positive integer 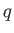 , then
we have
, then
we have
- Let
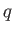 be a positive integer.
If
be a positive integer.
If 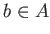 satisfies
satisfies
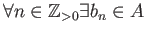
such that
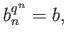
then we have
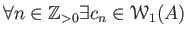
such that
![% latex2html id marker 628
$\displaystyle c_n^{q^n}=[b].
$](img16.png)
Recall that the ring of  -adic Witt vectors is a quotient of
the ring of universal Witt vectors. We have therefore a projection
-adic Witt vectors is a quotient of
the ring of universal Witt vectors. We have therefore a projection
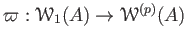 .
But in the following we intentionally omit to write
.
But in the following we intentionally omit to write 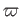 .
.
Since any integral domain can be embedded into a perfect field,
we deduce the following
COROLLARY 10.4
Let 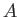 be an integral domain of characteristic
be an integral domain of characteristic 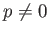 .
Then
.
Then
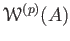 is an integral domain of characteristic 0
.
is an integral domain of characteristic 0
.
PROOF..
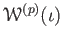
is always an injection when
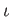
is.
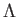
ARRAY(0x35e8850)ARRAY(0x35e8850)



Next: About this document ...
Yoshifumi Tsuchimoto
2016-06-18
![]() -adic Witt vectors is a quotient of
the ring of universal Witt vectors. We have therefore a projection
-adic Witt vectors is a quotient of
the ring of universal Witt vectors. We have therefore a projection
![]() .
But in the following we intentionally omit to write
.
But in the following we intentionally omit to write ![]() .
.
![% latex2html id marker 647
$\displaystyle \sum_{j=0}^\infty V_p^j ([x_j]) \qquad (x_j \in A).
$](img21.png)
![$\displaystyle \varphi: \mathcal W^{(p)}(A) \ni
\sum_{j=0}^\infty V_p^n ([x_j])
\mapsto x_0 \in A
$](img24.png)