


Next: About this document ...
Up: , , and the
Previous: The ring of -adic
In the preceding subsection we have described how the ring
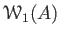 of universal Witt vectors decomposes into a countable direct sum of
the ring of
of universal Witt vectors decomposes into a countable direct sum of
the ring of 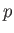 -adic Witt vectors. In this subsedtion we show that
thering
-adic Witt vectors. In this subsedtion we show that
thering
 can be defined for any ring
can be defined for any ring 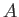 (that means,without
the assummption of
(that means,without
the assummption of 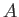 being characteristic
being characteristic 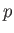 ).
).
We need some tools.
DEFINITION 9.11
Let
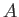
be any commutative ring.
Let
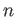
be a positive integer. Let us define additive operators

on
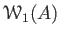
by the following formula.
(The latter definition is a formal one. It certainly makes sense
when
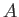
is an algebra over

. Then the definition descends to
a formal law defined over

so that

is defined for any ring
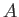
.
In other words,

is
actually defined to be the unique continuous additive map which
satisfies
)
LEMMA 9.12
Let 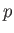 be a prime number.
Let
be a prime number.
Let 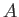 be acommutative ring of characteristic
be acommutative ring of characteristic 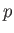 .
Then:
.
Then:
- We have
in partucular,  is an algebra endomorphism of
is an algebra endomorphism of
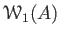 in this case.
in this case.
DEFINITION 9.13
Let
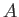
be any commutative ring.
Let
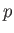
be a prime number.
We denote by
and define
by
LEMMA 9.14
Let us define polynomials
![$ \alpha_j(X,Y)\in \mathbb{Z}[X,Y]$](img101.png) by the following relation.
by the following relation.
Then we have the following rule for ``carry operation'':
PROPOSITION 9.15
There exist unique binary operators  and
and  on
on
 such that the following diagrams commute.
such that the following diagrams commute.
PROOF..
Using the rule as in the previous lemma, we see that addition descends to
an addition
of

.
It is easier to see that the multiplication also descends.

DEFINITION 9.16
For any commutative ring
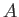
,
elements of

are called
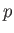 -adic Witt vectors
-adic Witt vectors over
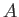
.
The ring

is called
the ring of 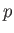 -adic Witt vectors
-adic Witt vectors over
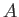
.
LEMMA 9.17
Let 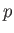 be a prime number.
Let
be a prime number.
Let 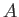 be a ring of characteristic
be a ring of characteristic 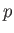 .
Then for any
.
Then for any 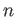 which is not divisible by
which is not divisible by 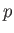 , the map
, the map
is a ``non-unital ring homomorphism".
Its image is equal to the range of the idempotent
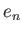 . That means,
. That means,
PROOF..

is already shown to be additive. The following calculation
shows that

preserves the multiplication:
for any positive integer

with lcm
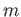
and for any element

,
we have:
We then notice that the image of the unit element
![$ [1]$](img25.png)
of the
Witt algebra is equal to
![$ \frac{1}{n}V_n ([1] )= e_n$](img121.png)
ant that

for any

.
The rest is then obvious.

In preparing from No.7 to No.10 of this lecture,
the following reference (especially its appendix) has been useful:
http://www.math.upenn.edu/~chai/course_notes/cartier_12_2004.pdf



Next: About this document ...
Up: , , and the
Previous: The ring of -adic
docky
2016-06-18






![]()





