пњљпњљпњљпњљ
![]() ,
,
![]() пњљ»§пњљпњљпњљпњљ»§пњљпњљпњљ
пњљ»§пњљпњљпњљпњљ»§пњљпњљпњљ
![]()
![]() ,
,
![]() пњљ §пњљпњљ
пњљ §пњљпњљ
[пњљпњљпњљпњљ] пњљпњљпњљќ•пњљпњљ∆•√•„§«Њпњљпњљпњљпњљпњљпњљл°£
пњљпњљќ§и§¶пњљЋ°пњљ пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ§√§пњљпњљпњљ«§ §й°Ґпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ∆§пњљ ђпњљпњљпњљпњљд§єпњљпњљпњљ §л°£ (пњљпњљпњљпњљпњљпњљпњљкЉЂпњљќ§ѕ°пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќєпњљпњљџ§пњљпњљќ§пњљќ§пњљ…ђпњљ„§«§пњљпњљ√§пњљпњљќ§«°пњљ пњљпњљпњљпњљпњљпњљпњљќіпњљпњљпњљпњљпњљпњљпњљ(пњљпњљпњљпњљпњљпњљпњљ–±пњљ)пњљпњљпњљ—§пњљпњљпњљпњљЋЊпњљпњљпњљпњљпњљпњљпњљ…ђпњљ„§пњљпњљпњљпњљ√§пњљпњљпњљ)
пњљпњљя§пњљпњљпњљ
пњљпњљ≈ЇпњљпњљпњљЋ§ƒ§пњљпњљ∆°пњљ
пњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљл°£
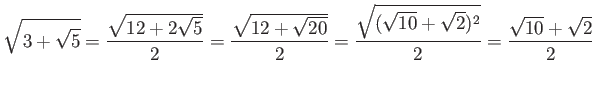
пњљƒ§ё§к°Ґ
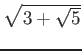 пњљѕ°пњљпњљпњљпњљ’§ќ§и§¶пњљЋіпњљ√±пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљ≈Їпњљпњљпњљпњљѕ§пњљпњљпњљпњљ»§пњљпњљпњљпњљпњљ
∆±пњљЌ§Ћ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ©пњљƒ§пњљпњљ»§пњљпњљп§Ђпњљл°£
пњљѕ°пњљпњљпњљпњљ’§ќ§и§¶пњљЋіпњљ√±пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљ≈Їпњљпњљпњљпњљѕ§пњљпњљпњљпњљ»§пњљпњљпњљпњљпњљ
∆±пњљЌ§Ћ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ©пњљƒ§пњљпњљ»§пњљпњљп§Ђпњљл°£
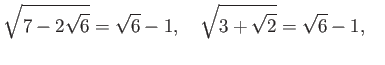
пњљпњљпњљпњљпњљ«°пњљ
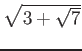 пњљѕЊпњљќ§и§¶пњљЋ§ѕіпњљ√±пњљЋ§ §пњљ §пњљпњљпњљ
пњљпњљпњљпњљѕ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљѕЊпњљќ§и§¶пњљЋ§ѕіпњљ√±пњљЋ§ §пњљ §пњљпњљпњљ
пњљпњљпњљпњљѕ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
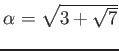 пњљпњљ
пњљпњљпњљ»§пњљпњљ∆іё§пњљпњљќ§ѕ°пњљ
пњљпњљ
пњљпњљпњљ»§пњљпњљ∆іё§пњљпњљќ§ѕ°пњљ
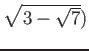 пњљвЄµпњљ»§пњљпњљ∆іё§а°£
пњљвЄµпњљ»§пњљпњљ∆іё§а°£
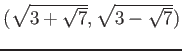 .
.
[пњљпњљпњљпњљпњљпњљпњљ–±пњљпњљќЊпњљпњљпњљ]
пњљпњљ ![]() пњљќ•пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљќ•пњљпњљпњљпњљпњљпњљпњљпњљпњљ ![]() пњљпњљЌњпњљпњљпњљпњљпњљ∆§пњљпњљпњљ»§пњљпњљл°£
пњљпњљЌњпњљпњљпњљпњљпњљ∆§пњљпњљпњљ»§пњљпњљл°£
![]() пњљпњљпњљпњљ ђпњљпњљ
пњљпњљпњљпњљ ђпњљпњљ ![]() пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљпњљпњљпњљпњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљпњљл°£пњљпњљпњљќїпњљпњљпњљпњљпњљпњљќ§пњљпњљ»§пњљпњљпњљпњљпњљќ©пњљƒ°пњљ(√±ƒіпњљпњљпњљпњљпњљпњљ)
пњљ¬§ѕ°пњљпњљпњљпњљ (1)-(4) пњљпњљпњљй°Ґпњљпњљпњљпњљпњљпњљпњљпњљ≈™пњљ Ј„їпњљпњљ«Љпњљпњљќ§пњљпњљ»§пњљпњљпњљпњљпњљќ©пњљƒ§пњљпњљ»§пњљпњљп§Ђпњљл°£
("3пњљпњљ=1пњљпњљ")
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ«§ѕ°пњљпњљпњљпњљпњљЋЉпњљпњљќ§пњљпњљ»§пњљ ђпњљпњљпњљл°£(пњљпњљпњљпњљ√±ƒіпњљпњљпњљпњљпњљпњљ)
(пњљпњљпњљпњљ9.4пњљЋ§пњљл°£)
(ћњпњљпњљ8.4пњљЋ§пњљл°£)
пњљпњљпњљќ§пњљпњљ»§пњљпњљй°Ґпњљ«ЄпњљЋЉпњљпњљќ§пњљпњљ»§пњљ ђпњљпњљпњљл°£
("2пњљпњљ=0пњљпњљ")