�����Υơ���:
![]()
�ʲ�����������Τ������뤳�Ȥ�������濴�ˤʤ롣
��¸���� ![]() �ˤ������ơ�
���ξ�����Ū�ʸ�
�ˤ������ơ�
���ξ�����Ū�ʸ� ![]() ���դ��ä��ƿ�������
���դ��ä��ƿ������� ![]() ��
�Ĥ��뤳�Ȥ��Ǥ���ΤǤ��ä���
�����
��
�Ĥ��뤳�Ȥ��Ǥ���ΤǤ��ä���
����� ![]() ��
�� ![]() ��κǾ�¿�༰
��κǾ�¿�༰ ![]() ���Ѥ��ƺ����
���Ѥ��ƺ����
�Ȥ�����;�Ĥ�Ʊ���Ǥ��롣 �äˤ���Ʊ�����
���̤ˡ�Ϳ����줿¿�༰ ![]() ���Ф��ơ�
���Ф��ơ�![]() �κ�����
�κ����� ![]() �˲ä��뤳�Ȥˤ�ꡢ
�˲ä��뤳�Ȥˤ�ꡢ
![]() ��ʬ���Τ��뤳�Ȥ��Ǥ����ʤ���Ť��Ǿ�ʬ���Τ�
��ʬ���Τ��뤳�Ȥ��Ǥ����ʤ���Ť��Ǿ�ʬ���Τ�
![]() �ˤ�ä�Ʊ��������ư�դ˷�ޤ�ΤǤ��ä���
�ˤ�ä�Ʊ��������ư�դ˷�ޤ�ΤǤ��ä���
ʬΥ��������ؤ�ʤ�dzؤӤ����ԤˤȤäƤ�����ʳ�ǰ�Ǥ��뤬��
���ν��������갷�����ϰ�ö�����������˽��Ϥ��Ƥ���Τۤ���
�褯ʬ����褦�˻פ��롣�������äƤ��ιֵ��Ǥ�
����ȡ���ɸ�� 0
�ΤȤ��פˤĤ��Ƥ����դƤ����˻ߤ�褦��
(�� ![]() �ˤ����ơ�
�ˤ����ơ�![]() ������ 0
�ˤʤ��礬���롣
���Τ褦�ʡֲ���פ�
������ 0
�ˤʤ��礬���롣
���Τ褦�ʡֲ���פ� ![]() ��ɸ���Ȥ�֡���äȥ��å��襯������
���Τ褦�ˤʤ롣)
��ɸ���Ȥ�֡���äȥ��å��襯������
���Τ褦�ˤʤ롣)
�γˤ� 0 ����
�㤨���ǿ� ![]() ��Ϳ�����Ȥ���
��Ϳ�����Ȥ���
![]() �� ɸ��
�� ɸ�� ![]() �Ǥ��롣
�Ǥ��롣
![$\displaystyle \frac{d}{d X} : K[X] \to K[X]
$](img16.png)
��
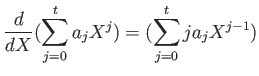
��������롣
���̿��ˤ�ꡢ
![]() �ʤ��
�ʤ�� ![]() ����������Τ�ɬ��
����������Τ�ɬ�� ![]() ��
ʬΥŪ�Ǥ���
��
ʬΥŪ�Ǥ���
ʬΥ����ռ�����Ȥ����������ä��饯�ˤ����ࡣ�㤨��:
��ߤ���
�ϼºݤˤϤ����Ĥθ�
�Ȥ���ҤȤĤ�������������롣
�Ǥ��뤳�Ȥ�������衣
����
�Ǥ��뤳�Ȥ��ʤ�����
��ߤ����褦��