


Next: About this document ...
�����Ƚ������� No.��8
����������Ȥ��ˡ��֥ۥƥ�ҥ�٥�ȡפΤ褦�ʲ���Ǥ���ΤǤ�����
���β��Ǥϡ����ͤϡ��ֶ��������ʤ����ȡפ��б�����
ñ�ͤϡ��ֳ������ļ���(ñ�ͤǤʤ����Ȥϡ�
�������������뤳��)���б�����ΤǤ�����
���ͤ�ñ�ͤ�¸�ߤϡ��Ͻ���Ƚ�����θ���¿���ȴط����Ƥ���ΤǤ�����
&dotfill#dotfill;
��8���ܤμ��� :

���������
��� �� 8.1
����
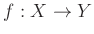
��
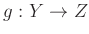
��Ϳ�����Ƥ���Ȥ��롣
���ΤȤ���
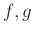
��
��������
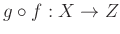
��
��������롣
����̿��ϴ�ñ�ǤϤ��뤬ͭ�ѤǤ��롣���Ѿ�Ϥ��Τ褦��̿�꤬���뤳�Ȥ���
�������Ƥ����ơ���������Ƭ����dzΤ����Τ�������������
��� �� 8.3
����
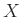
���Ф��ơ�����
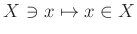
��
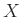
��
���������Ȥ�����
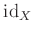
��ɽ����
���̿��⡢
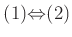 �ʳ��Ϥ������ٳ�ǧ������ɤ���
�ʳ��Ϥ������ٳ�ǧ������ɤ���
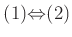 ���ä˽��פǤ��롣
���ä˽��פǤ��롣
���� �� 8.2
![$ X={\mathbb{C}}[t] $](img25.png)
(ʣ�ǿ�������
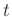
���ѿ��Ȥ���¿�༰�����ΤΤʤ�����),
![$ Y={\mathbb{C}}[t]$](img27.png)
�Ȥ�����
����
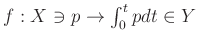
��
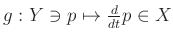
�ˤ������ơ�
-
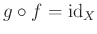 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
-
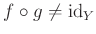 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
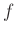 ,
, 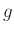 �Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������
�Ϥ��줾�����͡�ñ�͡���ñ�ͤ���������



Next: About this document ...
2015-06-11
![]()