


Next: About this document ...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Č―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― No.13
ïŋ―ïŋ―13ïŋ―ïŋ―ïŋ―ÜĪΞïŋ―ïŋ―ïŋ― : ïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(3)ïŋ―ÎĪčĪĶïŋ―Ęūïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―
ïŋ―Öžïŋ―ïŋ―ïŋ― 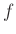 ïŋ―ïŋ― ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―éĪšïŋ―ËĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČļÆĪÐĪïŋ―ÆĪČĪïŋ―ïŋ―Ë―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ― ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―éĪšïŋ―ËĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČļÆĪÐĪïŋ―ÆĪČĪïŋ―ïŋ―Ë―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ÄĪïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪÏ―ïŋ―ïŋ―ïŋ―Î―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ÆĪÐĪėĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ØĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ØĪĘĪÉĪÎģïŋ―ĘŽïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
Ėŋïŋ―ïŋ― 13.1
ïŋ―ïŋ―ïŋ―ïŋ―
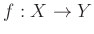
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ėĪŋïŋ―ČĪïŋ―ïŋ―ïŋ―
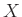 ïŋ―ïŋ―Æąïŋ―ÍīØ·ïŋ―
ïŋ―ïŋ―Æąïŋ―ÍīØ·ïŋ― 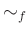 ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
-
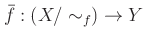 ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ËĪïŋ―ęĪĶïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―![$ [x]_f$](img26.png) ïŋ―ïŋ―
ïŋ―ïŋ― 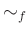 ïŋ―ËīØĪïŋ―ïŋ―ïŋ―
ïŋ―ËīØĪïŋ―ïŋ―ïŋ― 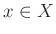 ïŋ―ÎĨïŋ―ïŋ―éĨđïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÎĨïŋ―ïŋ―éĨđïŋ―ĮĪïŋ―ïŋ―ëĄĢ
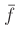 ïŋ―ïŋ―
ïŋ―ïŋ― 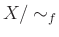 ïŋ―ïŋ―
ïŋ―ïŋ―
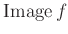 ïŋ―ČĪÎīÖĪïŋ―ïŋ―ïŋ―Ãąïŋ―ÍĪïŋ―Íŋïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ČĪÎīÖĪïŋ―ïŋ―ïŋ―Ãąïŋ―ÍĪïŋ―Íŋïŋ―ïŋ―ïŋ―ëĄĢ
-
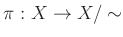 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ÆĪČĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ÆĪČĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
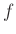 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―Ãąïŋ―ÍĪÎđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ĘŽïŋ―ōĪĩĪïŋ―ëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―Ãąïŋ―ÍĪÎđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ĘŽïŋ―ōĪĩĪïŋ―ëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―



Next: About this document ...
2015-07-23
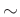 ïŋ―ïŋ―Æąïŋ―ÍīØ·ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Æąïŋ―ÍīØ·ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
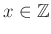 ïŋ―ïŋ―
ïŋ―ïŋ― 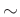 ïŋ―ËīØĪïŋ―ïŋ―ëĨŊïŋ―éĨđïŋ―ïŋ―
ïŋ―ËīØĪïŋ―ïŋ―ëĨŊïŋ―éĨđïŋ―ïŋ― ![$ [x]$](img5.png) ïŋ―Č―ņĪŊĄïŋ―
ïŋ―Č―ņĪŊĄïŋ―
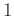 ïŋ―ÎĨïŋ―ïŋ―éĨđ
ïŋ―ÎĨïŋ―ïŋ―éĨđ ![$ [1]$](img7.png) ïŋ―ïŋ―°ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―°ïŋ―ïŋ―ïŋ―ïŋ―
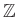 ïŋ―Îļïŋ―ïŋ―ōĪđĪŲĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Îļïŋ―ïŋ―ōĪđĪŲĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
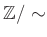 ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
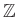 ïŋ―ØĪΞïŋ―ïŋ―ïŋ―
ïŋ―ØĪΞïŋ―ïŋ―ïŋ―  ïŋ―ïŋ―
ïŋ―ïŋ―
![$ f([x])=$](img10.png) ($x$ ïŋ―ïŋ― $3$ ïŋ―Įģïŋ―ÃĪïŋ―Íūïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
($x$ ïŋ―ïŋ― $3$ ïŋ―Įģïŋ―ÃĪïŋ―Íūïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
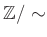 ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
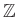 ïŋ―ØĪΞïŋ―ïŋ―ïŋ―
ïŋ―ØĪΞïŋ―ïŋ―ïŋ― 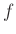 ïŋ―ïŋ―
ïŋ―ïŋ―
![$ f([x])=$](img10.png) ($x$ ïŋ―ïŋ― $4$ ïŋ―Įģïŋ―ÃĪïŋ―Íūïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
($x$ ïŋ―ïŋ― $4$ ïŋ―Įģïŋ―ÃĪïŋ―Íūïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―