-
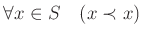
-
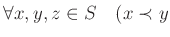 and
and 
魹スハイ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ、魹ス魹スミア魹スハェ魹ス魹ス㖨ッ。魹ス
![]() 魹スヒ、マ。魹ス魹ス魹ス魹スホ、隍ヲ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スリキ魹ス魹ス魹ス魹ス魹ス魹ス槩」
魹スヒ、マ。魹ス魹ス魹ス魹スホ、隍ヲ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スリキ魹ス魹ス魹ス魹ス魹ス魹ス槩」
![]() 魹ス魹スニア魹スヘエリキ魹ス
魹ス魹スニア魹スヘエリキ魹ス ![]() 魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス槩」
![]() 魹スネ、マ。魹ス
魹スネ、マ。魹ス ![]() 魹ス魹ス
魹ス魹ス ![]() 魹スホソ魹ス魹スフ、ヌ、魹ス魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス魹スネ、ヌ、魹ス魹ス魹ス
魹スホソ魹ス魹スフ、ヌ、魹ス魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス魹スネ、ヌ、魹ス魹ス魹ス
ニア魹スヘエリキ魹ス魹スヒ、魹ス遙「![]() 魹ス魹ス魹ス魹ス魹ス鬣ケハャ魹ス魹ス魹ス魹ス魹ス魹ス槩」
魹スニ・魹ス魹ス鬣ケ魹スマ。ヨソ魹スツイ魹スラ、ヌ、魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス鬣ケハャ魹ス魹ス魹ス魹ス魹ス魹ス槩」
魹スニ・魹ス魹ス鬣ケ魹スマ。ヨソ魹スツイ魹スラ、ヌ、魹ス魹ス魹ス
魹ス魹ス魹ス鬣ケ
![]() 魹ス魹ス魹スネ、魹ス
魹ス魹ス魹スネ、魹ス
![]() 魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス ![]() 魹スリ、ホシ魹ス魹ス魹ス
魹スリ、ホシ魹ス魹ス魹ス ![]() 魹スネ、魹ス魹スホオユシ魹ス魹ス魹ス
魹スネ、魹ス魹スホオユシ魹ス魹ス魹ス ![]() 魹ス魹ス魹スネ、魹スホゥ魹スニ、隍ヲ魹ス魹ス
魹ス魹ス魹スト、ホ・魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス槩」
魹ス魹ス魹スネ、魹スホゥ魹スニ、隍ヲ魹ス魹ス
魹ス魹ス魹スト、ホ・魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス槩」
Case I: ![]() 魹スヒコヌセ魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス遑」
魹スヒコヌセ魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス遑」
魹ス魹ス魹スホ、ミ、魹ス魹ス魹ス魹ス魹ス
![]() 魹スヌ、魹ス魹ス槩」
魹スヌ、魹ス魹ス槩」
魹スネシ魹ス魹ス魹ス魹スノ、魹ス魹ス魹ス
Case II. ![]() 魹スヒコヌセ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス遑」
魹スヒコヌセ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス遑」
魹ス魹ス魹スホコヌセ魹ス魹ス魹ス魹ス魹ス ![]() 魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス
![]() 魹スマク゚、魹ス魹ス魹ス魹ス魹スロ、ハ、槩」
魹スマク゚、魹ス魹ス魹ス魹ス魹スロ、ハ、槩」
魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス
![]() 魹スハ、ホ、ヌ、魹ス魹ス槩」
魹スハ、ホ、ヌ、魹ス魹ス槩」
![]() 魹ス魹ス魹ステ、魹ス魹ス魹ス魹ス鬘「
魹ス魹ス魹ステ、魹ス魹ス魹ス魹ス鬘「
![]()
![]() .
.
![]() 魹ス魹ス魹スン、魹ス魹スヒ、魹ステ、ニ、ユ、魹ス魹スネ、魹ス魹ス魹スヒセ魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス槩」
魹ス魹ス魹スン、魹ス魹スヒ、魹ステ、ニ、ユ、魹ス魹スネ、魹ス魹ス魹スヒセ魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス槩」
Case II-1).
![]() 魹スホ、ネ、魹ス魹ス魹ス
魹スホ、ネ、魹ス魹ス魹ス
![]() 魹スヌ、魹ス魹ス槩」
魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ステ、ニ。魹スCase I 魹ス魹スニア魹ス魹ス魹ス魹ス
魹スネシ魹ス魹ス魹ス魹スノ、魹ス魹ス魹ス
Case II-2).
![]() 魹スホ、ネ、魹ス魹ス魹ス
魹スホ、ネ、魹ス魹ス魹ス
魹ス魹ス魹スホ、ネ、魹ス魹スホ、゚。魹ス![]() 魹ス魹ス
魹ス魹ス
![]() 魹スホエヨ、ヒー网、魹ス魹ス魹ス魹ス魹ス魹ス魹ス槩」
魹スホエヨ、ヒー网、魹ス魹ス魹ス魹ス魹ス魹ス魹ス槩」
![]() 魹ス魹ス
魹ス魹ス
![]() 魹スネ、魹ス魹ス魹ステア魹スヘ、魹スヘソ魹ス魹ス魹ス魹スヒ、マ。魹ス魹ス魹スト、魹ス魹ス鬢サ魹ス魹ス魹スノ、魹ス魹ス魹ス
魹スネ、魹ス魹ス魹ステア魹スヘ、魹スヘソ魹ス魹ス魹ス魹スヒ、マ。魹ス魹ス魹スト、魹ス魹ス鬢サ魹ス魹ス魹スノ、魹ス魹ス魹ス
魹ス魹ス魹ス魹ステア魹スヘ、ヌ、魹ス魹ステ、ニ。魹ス魹ス魹ス魹スホオユシ魹ス魹ス魹ス魹ス魹ス
魹スネシ魹ス魹ス魹ス魹スノ、魹ス魹ス魹ス
魹ス魹スホセ魹ス魹ス魹ス魹ス魹ス 魹ス魹ス魹ス鬣ケハャ魹ス魹ス魹スホコン、魹ス 魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、テ、ニ、魹ス魹ス槩」 魹スツコン、ヒ、マ。魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、魹スハ、魹ス魹スニ、魹スム、魹スホ、ヌ。魹ス 魹ス魹ス魹ス魹スマセ魹ス魹ス魹ス魹スヨシ魹ス゚。ラ、ネク魹ス魹ス魹ス魹ス槶ォ魹ス筅キ魹ス魹スハ、魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、顬コ魹スヒセ魹ス魹ス魹ス魹ス魹ス魹ス魹スヒ、マ。魹ス魹ス魹ス魹スホ、隍ヲ魹スヒケヘ、魹ス魹ス槩」
![]() 魹スネ、魹ス魹ス魹ス魹ス魹ス
魹スネ、魹ス魹ス魹ス魹ス魹ス
![]() 魹ス魹ス 魹スリ、魹ス魹スホ、ハ、魹ス魹ス魹ストケマキ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、ホス魹ス魹ス魹スヒ、魹ス魹ス魹ス魹ス槩」
魹ス魹ス 魹スリ、魹ス魹スホ、ハ、魹ス魹ス魹ストケマキ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、ホス魹ス魹ス魹スヒ、魹ス魹ス魹ス魹ス槩」
魹ス魹ス魹ス魹スヒ。魹ス
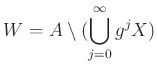
魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス [
魹ス魹ス魹スニ。魹ス
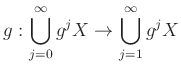
魹ス魹ス魹ス魹ステア魹スヘ、ヌ、魹ス魹ス槩」
魹ス魹ス魹スホ、魹ス魹スネ、魹ス魹スニーラ、魹スハャ魹ス魹ス魹ス槩」
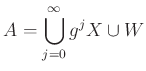
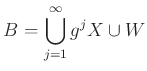
魹ス魹ステ、ニ。魹ス
魹ス魹ス魹スホ・鬣、魹ス晫ャ。魹ス 魹スワケヨオ魹ス魹スホカ魹ス魹スハス魹ス(魹ス魹ス魹スモ。魹ス魹ス髹ォ魹ス魹ス魹ス魹ス魹スヨス魹ス魹ス魹スネー魹ス魹ス魹ス魹ス魹スヨ、ホエ魹ス魹ステ。魹ス魹ス魹ス魹スワ。魹ス)魹スヒ、魹ス魹ス魹ス魹ス魹ス魹ス 魹スヌ、魹ス魹ス槩」魹ス魹ス魹ス魹ス魹スハ、魹スル、魹ス魹ス魹ス魹ス顬サ魹スニ、魹ス魹ス槩」魹スワコル、マカ魹ス魹スハス魹ス忋イセネ、ホ、魹ス魹スネ。魹ス