![]()
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŽïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ØĪΞïŋ―ïŋ―ïŋ―
ïŋ―ØĪΞïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ØĪΞïŋ―ïŋ―ïŋ―
ïŋ―ØĪΞïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪëĄĢ
ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ØĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ØĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ÏĄïŋ―
ïŋ―ÏĄïŋ―![]() ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ØĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―ïŋ―Î―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŽïŋ―ŅĪĮĪïŋ―ïŋ―ÆĄïŋ―
(ïŋ―ïŋ―ËĄ)ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―
ïŋ―ØĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―ïŋ―Î―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŽïŋ―ŅĪĮĪïŋ―ïŋ―ÆĄïŋ―
(ïŋ―ïŋ―ËĄ)ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïĪŦïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÄĪÏĪïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÖĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÚĪïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪČžïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÛĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―饞ïŋ―ÜĪïŋ―ÍĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïĪŦïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÄĪÏĪïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÖĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÚĪïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪČžïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÛĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―饞ïŋ―ÜĪïŋ―ÍĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―
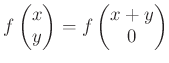
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―