![]() �������η���������ʬ����
�������η���������ʬ����
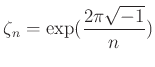 �Ȥ�����
ʣ��ʿ�̤��餽�켫�Ȥؤ���ñ�ͤΤ�����
�Ȥ�����
ʣ��ʿ�̤��餽�켫�Ȥؤ���ñ�ͤΤ�����
![]() ���ɽ���ˤϤ����Ĥ���ˡ�����롣
���ɽ���ˤϤ����Ĥ���ˡ�����롣
�� �������ȴط����ˤ��ɽ����
![]() �η��黻������ˤϡ�
�η��黻������ˤϡ�
![]() ��������ɤ��Ȥ������Ȥ�ʬ���롣���Τ��ߤǡ�
��������ɤ��Ȥ������Ȥ�ʬ���롣���Τ��ߤǡ�
�Ƚ�
�� �ִ��Ȥ��Ƥ�ɽ��
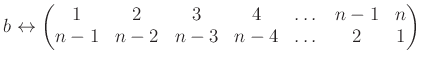
�Ȥ����б��ˤ��
��
�¹���Ȥ��Ƥ�ɽ����
![]() �ϤȤ��
�ϤȤ��
![]() ����
����
![]() �ؤμ����������Ǥ��뤳�Ȥ����ܤ��롣
�ؤμ����������Ǥ��뤳�Ȥ����ܤ��롣
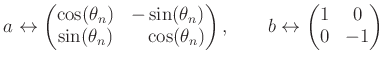
(�
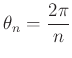 )
)
![]() ����Ĵ��ʷ��Ǥ��롣���̤ˡ���Ĵ��η�����ʬ����
���(���饹ʬ������)�ݤˤϺ��������̤�ɬ�פǤ��롣
����Ĵ��ʷ��Ǥ��롣���̤ˡ���Ĵ��η�����ʬ����
���(���饹ʬ������)�ݤˤϺ��������̤�ɬ�פǤ��롣
�ΤȤ��ˤ����������Ʊ�ʹط���������롣����Ʊ����ν����
Ʊ�ͤˡ���Ʊ�͡�![]() ���������롣
���������롣
![]() �Ͻ���κ��ε���
�Ͻ���κ��ε���
![]() �Ȥ褯���Ƥ��뤬��
��Ԥ϶�����Ǥ��뤫��ޤ��Ȥ�ʤ������ʤ������äȹͤ���ж��̤��Ĥ���
�Ȥ褯���Ƥ��뤬��
��Ԥ϶�����Ǥ��뤫��ޤ��Ȥ�ʤ������ʤ������äȹͤ���ж��̤��Ĥ���
�����饹ʬ����
�Ǥ��ꡢ���ĤΥ��饹ʬ����(�¤�)���פ��롣
�����饹ʬ����
�Ǥ��뤬��2�ĤΥ��饹ʬ���ϰ��פ��ʤ���
�� ![]() �ξ�;��ˤ�륯�饹ʬ���ϡ���äȶ���Ū��(�㤨�С�������Ū��)
��̣���Ĥ����Ȥ�¿�����㤨��
�ξ�;��ˤ�륯�饹ʬ���ϡ���äȶ���Ū��(�㤨�С�������Ū��)
��̣���Ĥ����Ȥ�¿�����㤨��
![]() �� ��ǡ�
�� ��ǡ�