


Next: sheaves
zeta functions
Yoshifumi Tsuchimoto
DEFINITION 10.1
For any commutative ring
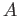
, we define its
spectrum as
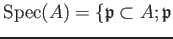
is a prime ideal of $A$
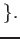
For any subset
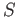
of
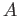
we define
Then we may topologize

in such a way that the closed
sets are sets of the form

for some
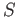
. Namely,
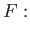
closed

We refer to the topology as the
Zariski topology.
EXERCISE 10.1
Prove that Zariski topology is indeed a topolgy.
That means, the collection

satisfies the axiom of closed sets.
PROPOSITION 10.3
For any ring homomorphism
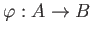 , we have a map
, we have a map
It is continuous with respect to the Zariski topology.
DEFINITION 10.5
Let
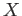
be a topological space. A closed set
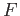
of
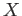
is said to be
reducible if there exist closed sets
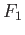
and
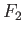
such that
holds.
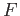
is said to be
irreducible if it is not reducible.
DEFINITION 10.6
Let
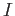
be an ideal of a ring
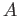
. Then we define its
radical to be
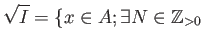
such that
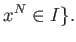
PROPOSITION 10.7
Let 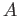 be a ring. Then;
be a ring. Then;
- For any ideal
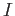 of
of 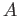 , we have
, we have
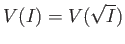 .
.
- For two ideals
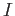 ,
, 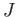 of
of 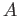 ,
,
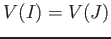 holds if and only if
holds if and only if
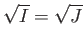 .
.
- For an ideal
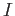 of
of 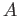 ,
,
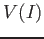 is irreducible if and only if
is irreducible if and only if 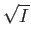 is a prime ideal.
is a prime ideal.
It is knwon that
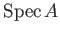 has a structure of ``locally ringed space''.
A locally ringed space which locally lookes like an affine spectrum of a ring
is called a scheme.
has a structure of ``locally ringed space''.
A locally ringed space which locally lookes like an affine spectrum of a ring
is called a scheme.
DEFINITION 10.8
Let

be a
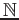
-graded ring.
We put

.
We define
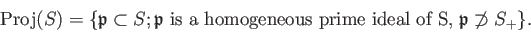
It is known that
 carries a ringed space strucure on it and
that it is a scheme.
carries a ringed space strucure on it and
that it is a scheme.
DEFINITION 10.9
Let
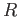
be a ring. Let
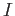
be an ideal of
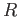
.
The scheme
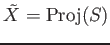
associated to the
graded ring

is called
the blowing up of
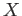
with respect to
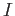
.




Next: sheaves
2015-06-29
![]()
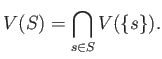
![]() has a structure of ``locally ringed space''.
A locally ringed space which locally lookes like an affine spectrum of a ring
is called a scheme.
has a structure of ``locally ringed space''.
A locally ringed space which locally lookes like an affine spectrum of a ring
is called a scheme.
![]()
![]() carries a ringed space strucure on it and
that it is a scheme.
carries a ringed space strucure on it and
that it is a scheme.
![]()