Next: About this document ...
пњљпњљ ђпњљпњљ ђпњљЎ≥пњљпњљпњљAIпњљпњљпњљпњљ No.3
пњљпњљ3пњљпњљпњљ№§ќЉпњљпњљпњљ :

пњљпњљ¬Ђпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ 3.1 пњљ«љ“§ў§пњљпњљћ§пњљ«§пњљпњљл°£
пњљпњљпњљпњљ«§пњљпњљпњљпњљ 3.1 пњљпњљ»љпњљпњљЋ°пњљпњљпњљпњљпњљпњљпњљпњљ 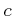 пњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 3.1
пњљпњљпњљпњљ
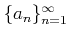
пњљпњљ
(пњљпњљпњљпњљЌ§пњљпњљќ§пњљпњљб§њпњљ»§пњљпњљпњљ)
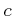
пњљЋЉпњљ¬Ђпњљпњљпњљпњљ
(пњљћ§ќњЌ§пњљпњљќ§пњљпњљб§њпњљ»§пњљпњљпњљ) 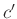
пњљЋ§пњљпњљ¬Ђпњљпњљпњљпњљ §й°Ґ
пњљ«§пњљпњљл°£пњљƒ§ё§к°ҐпњљпњљпњљпњљќЉпњљ¬Ђпњљпњљпњљ¬Єпњљя§пњљпњљпњљ»§пњљпњљпњљпњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљ §пњљпњљпњљ
пњљпњљпњљпњљпњљ«°пњљпњљƒ§пњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљпњљпњљ 3.2
пњљпњљпњљпњљ
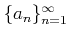
пњљпњљпњљпњљпњљпњљпњљ
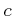
пњљЋЉпњљ¬Ђпњљпњљпњљпњљ»§пњљпњљпњљ
пњљ»љс§§§∆°пњљ
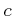
пњљќ§пњљпњљ»§пњљ
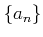
пњљпњљ
пњљЋЄпњљпњљ»Є∆§÷°пњљ
пњљпњљпњљпњљ 3.4
пњљпњљ¬ЂпњљпњљпњљпњљпњљпњљпњљпњљЌ≠пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљ 3.5
пњљ¬њпњљпњљпњљ
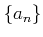
,
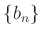
пњљѕ§пњљпњљм§Њпњљпњљпњљ¬Ђпњљпњљпњљпњљ»§пњљпњљл°£пњљпњљпњљќ§»§пњљпњљпњљ
- пњљ÷ґЋЄ¬§пњљ»§пњљ„§»§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£пњљпњљпњљ §пњљпњљпњљпњљ
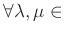
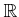 пњљпњљпњљ–§пњљпњљпњљ
пњљпњљпњљ–§пњљпњљпњљ
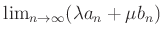 пњљѕЉпњљ¬Ђпњљпњљпњљ∆°пњљ
пњљѕЉпњљ¬Ђпњљпњљпњљ∆°пњљ
- пњљ÷Љ¬њпњљпњљќЊпњљЋ°пњљпњљѕҐ¬≥пњљ«§пњљпњљл°£пњљпњљ
- пњљ¬њпњљпњљќљпњљЋ°пњљѕ°пњљѕҐ¬≥пњљ„§«§пњљпњљл°£ пњљпњљ√§»Њ№§пњљпњљпњљпњљпњљпњљпњљпњљ»°пњљ
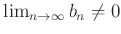 пњљ §й°Ґ
Ќ≠пњљ¬Єƒ§пњљпњљг≥∞пњљпњљпњљпњљпњљпњљпњљ
пњљ §й°Ґ
Ќ≠пњљ¬Єƒ§пњљпњљг≥∞пњљпњљпњљпњљпњљпњљпњљ 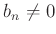 пњљ«§пњљпњљ√§∆°пњљ
пњљ«§пњљпњљ√§∆°пњљ
пњљпњљпњљпњљпњљпњљпњљпњљѕ°пњљпњљ…§пњљпњљй§Ђпњљ»§пњљпњљпњљпњљпњљпњљпњљпњљћ§пњљпњљпњљпњљ—њпњљпњљЎњпњљпњљпњљѕҐ¬≥пњљпњљпњљЋіЎ§пњљпњљпњљ
пњљпњљпњљпњљпњљ»§пњљпњљ∆∞пњљпњљпњљпњљџ§пњљпњљпњљпњљпњљпњљћ§пњљпњљпњљпњљ…§пњљпњљпњљ
пњљпњљпњљ—њпњљпњљЎњпњљпњљпњљѕҐ¬≥пњљпњљпњљЋ§ƒ§пњљпњљ∆§пњљпњљпњљ«ѓпњљпњљпњљпњљпњљЋЊ№Їў§Ћ≥Ў§÷§пњљпњљ»§Ћ§ §л§ђпњљпњљ
пњљпњљпњљпњљё§пњљпњљ‘§√§∆§пњљпњљпњљп§±пњљЋ§в§§пњљпњљпњљ §пњљпњљќ§«Њпњљќ§и§¶пњљ •пњљпњљ√•пњљпњљ÷°„§пњљпњљ—§пњљпњљпњљ
пњљ—§пњљпњљЏ§пњљ §пњљ…љпњљпњљ
пњљ«§ѕ§пњљпњљ√§∆§в§≥пњљпњљпњљЋљ“§ў§пњљ…ђпњљ„§пњљпњљпњљпњљ√§пњљпњљ»§пњљпњљпњљпњљп•±пњљпњљ
пњљпњљпњљпњљ 3.1
пњљ¬њпњљпњљпњљ
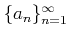
пњљпњљ
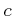
пњљЋЉпњљ¬Ђпњљпњљпњљпњљ»§пњљпњљпњљ
пњљѕЉпњљ¬Ђпњљпњљпњљпњљ»Єпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљ–§пњљпњљќЉпњљ¬ЂпњљпњљпњљпњљпњљЌ≥пњљт°ҐЄпњљпњљпњљпњљ §пњљпњљ §пњљпњљ
»њпњљпњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
(пњљпњљпњљпњљ: пњљпњљпњљпњљќє÷µпњљпњљ«Њпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљт§њ§пњљпњљ—§пњљпњљпњљќ§«§ѕ§ §пњљпњљпњљ
пњљпњљ¬Ђпњљпњљпњљпњљпњљпњљпњљпњљпњљ√§пњљ (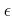 -
-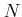 пњљпњљЋ°пњљпњљ)пњљпњљпњљпњљпњљпњљпњљл§≥пњљ»°пњљ)
пњљпњљЋ°пњљпњљ)пњљпњљпњљпњљпњљпњљпњљл§≥пњљ»°пњљ)
(пњљ“•пњљпњљ: 2пњљпњљпњљпњљпњљпњљ)
пњљпњљѕњ: пњљ÷њпњљпњљу§ђЉпњљ¬Ђпњљпњљпњљпњљ„§пњљпњљ»§ќЊпњљпњљпњљпњљќ•’•пњљпњљпњљпњљё•√•»°пњљ
пњљЌ≥—§пњљпњљпњљпњљпњљпњљпњљпњљпњљќ§пњљпњљпњљпњљ„°пњљпњљпњљпњљпњљ¬Њпњљпњљпњљ‘і÷§пњљпњљпњљЌ≥пњљ’§пњљпњљќ§пњљпњљпњљпњљ
Єпњљѕ§пњљпњљ…ђпњљ„§пњљпњљпњљпњљпњљпњљпњљв§Ґпњљл°£
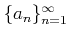 пњљпњљ
пњљпњљ 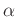 пњљЋЉпњљ¬Ђпњљпњљпњљл°£
пњљЋЉпњљ¬Ђпњљпњљпњљл°£
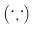
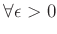 пњљпњљпњљ–§пњљпњљпњљ
пњљпњљпњљ–§пњљпњљпњљ
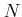 пњљ»§пњљпњљпњљ
пњљ»§пњљпњљпњљ
 пњљпњљпњљпњљ—§пњљпњљл°£
пњљпњљпњљпњљ»°пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ—§пњљпњљл°£
пњљпњљпњљпњљ»°пњљпњљпњљпњљпњљ 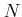 пњљпњљпњљпњљз§≠пњљпњљ«§пњљ’§пњљ
пњљпњљпњљпњљз§≠пњљпњљ«§пњљ’§пњљ 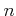 пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљ–§пњљпњљ∆°пњљ
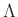
пњљпњљпњљпњљ 3.6
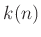
пњљпњљ
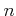
пњљтљљњ њпњљпњљпњљ…љпњљпњљпњљпњљпњљпњљпњљ»§пњљпњљќЈпњљпњљпњљ»§пњљпњљл°£
пњљ»§пњљпњљпњљпњљ»°пњљ
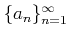
пњљпњљ 0
пњљЋЉпњљ¬Ђпњљпњљпњљл°£
ARRAY(0xad32748)



Next: About this document ...
2015-04-24
![]()
![]() пњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљпњљ
![]()
![]() пњљпњљпњљ–§пњљпњљпњљ
пњљпњљпњљ–§пњљпњљпњљ
![]() пњљ»§пњљпњљпњљ
пњљ»§пњљпњљпњљ
![]() пњљпњљпњљпњљ—§пњљпњљл°£
пњљпњљпњљпњљ»°пњљпњљпњљпњљпњљ
пњљпњљпњљпњљ—§пњљпњљл°£
пњљпњљпњљпњљ»°пњљпњљпњљпњљпњљ ![]() пњљпњљпњљпњљз§≠пњљпњљ«§пњљ’§пњљ
пњљпњљпњљпњљз§≠пњљпњљ«§пњљ’§пњљ ![]() пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљ–§пњљпњљ∆°пњљ