


Next: About this document ...
ïŋ―ïŋ―ïŋ―ïŋ―Øąé―Ž IB ïŋ―ïŋ―ïŋ―ïŋ― No.3

ïŋ―ïŋ―ïŋ― 3.1
ïŋ―ïŋ―

ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―įĪŽ

ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪÏĄïŋ―
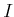 ïŋ―ïŋ―
ïŋ―ïŋ― 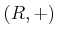 ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―÷ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―÷ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
-
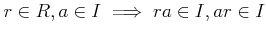
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïĪŽïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪČĪïŋ―ïŋ―Ëļïŋ―ïŋ―ïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.1
ïŋ―ïŋ―

ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―
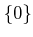
ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―Ėūïŋ―
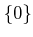
ïŋ―ïŋ―Ãąïŋ―ïŋ― 0
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪ·ïŋ―ÞĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ― 3.2
ïŋ―ïŋ―

ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―
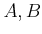
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
-
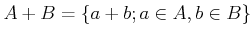 .
.
-
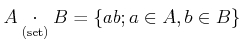 .
.
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―Âūïŋ―ïŋ―Ęķïŋ―ėĪŽïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ËĪÏĄïŋ―
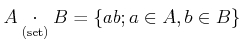
ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―
Ãąïŋ―ïŋ―
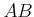
ïŋ―ČĪïŋ―ņĪĪÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.3
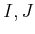
ïŋ―ïŋ―ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
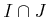
ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.4
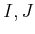
ïŋ―ïŋ―ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
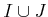
ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.5
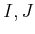
ïŋ―ïŋ―ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.6
![$ {\mbox{${\mathbb{Z}}$}}[X]$](img28.png)
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
![$ {\mbox{${\mathbb{Z}}$}}[X]$](img28.png)
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.7
![$ {\mbox{${\mathbb{Z}}$}}[X]$](img28.png)
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―
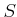
ïŋ―ĮĪïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ÂĄïŋ―ïŋ―ŅĪËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ËĪïŋ―ØĪïŋ―éĪšïŋ―ïŋ―
![$ {\mbox{${\mathbb{Z}}$}}[X]$](img28.png)
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪĘĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―óĪēĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.8
![$ {\mbox{${\mathbb{Z}}$}}[X]$](img28.png)
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
![$ {\mbox{${\mathbb{Z}}$}}[X]$](img28.png)
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.9
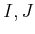
ïŋ―ïŋ―ïŋ―Äīïŋ―ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ËĪâĪŦïŋ―ïŋ―ïŋ―ïŋ―éĪš
(
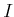
ïŋ―ïŋ―
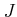
ïŋ―ïŋ―

ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ËĪĘĪïŋ―ĘĪïŋ―ïŋ―čĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.10
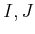
ïŋ―ïŋ―ïŋ―Äīïŋ―ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
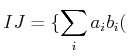
Íïŋ―ïŋ―ïŋ―ïŋ―
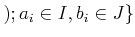
(ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ČĪĘĪëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(
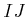
ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―
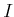
ïŋ―ïŋ―
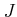
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ČļÆĪÖĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.11
ïŋ―Äīïŋ―ïŋ―ïŋ―

ïŋ―Îķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―

ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ČĪĘĪëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ― 3.3
Ãąïŋ―Ėļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄēÄīïŋ―ïŋ―ïŋ―

ïŋ―ïŋ―ΰïŋ―ïŋ―Ņŋïŋ―Âŋïŋ―āž°ïŋ―ČĪÏĄïŋ―
ïŋ―ÎĪčĪĶïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÎĪïŋ―ïŋ―ČĪĮĪïŋ―ïŋ―ïŋ―

ïŋ―ïŋ―ΰïŋ―ïŋ―Ņŋïŋ―Âŋïŋ―āž°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÏīÄĪïŋ―ĘĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―

ïŋ―ïŋ―ΰïŋ―ïŋ―Ņŋïŋ―Âŋïŋ―āž°ïŋ―ÄĪČļïŋ―ïŋ―ÃĪÆĄïŋ―
![$ R[X]$](img39.png)
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪ·ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―Ęēïŋ―ïŋ―ïŋ―ïŋ―ÝĪĘĪÎĪĮĄÔ°ïŋ―ïŋ―Ņŋïŋ―Âŋïŋ―āž°ïŋ―ÕĪïŋ―ïŋ―ÐĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪÏĄïŋ―

ïŋ―ïŋ―Ãąïŋ―Ėļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄēÄīïŋ―ïŋ―ÄĪĮĪïŋ―ïŋ―ïŋ―Čēïŋ―ïŋ―ęĪ·ïŋ―ÆĪïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.12 (Ãąïŋ―Ėļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄēÄīïŋ―)
ïŋ―ïŋ―

ïŋ―ïŋ―ΰïŋ―ïŋ―Ņŋïŋ―Âŋïŋ―āž°
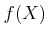
ïŋ―ïŋ―

ïŋ―Îļïŋ―
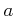
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―
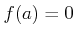
ïŋ―ĘĪïŋ―ÐĄïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïĪŧïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ― 3.4
ïŋ―ïŋ―

ïŋ―Îļïŋ―
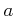
ïŋ―ÏĄïŋ―
ïŋ―ĘĪïŋ―
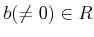
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČļÆĪÐĪïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ÍĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―Äīïŋ―ïŋ―ÄĪĮĪÏĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îķïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ÎĪĮĄïŋ―Ãąïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČļÆĪÓĪÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪïŋ― 0
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―Äīïŋ―ïŋ―ÄĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČļÆĪÓĪÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.13
ïŋ―ïŋ―ïŋ―ïŋ―

ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―Ņŋïŋ―Âŋïŋ―āž°
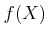
ïŋ―ÏĄïŋ―

ïŋ―ËđâĄđ
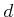
ïŋ―ÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.14
ïŋ―Äīïŋ―ïŋ―ïŋ―

ïŋ―ïŋ―ΰïŋ―ïŋ―Ņŋïŋ―Âŋïŋ―āž°
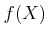
ïŋ―ηïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
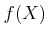
ïŋ―ïŋ―
![$ R[X]$](img39.png)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪČĪĘĪëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.15
Íïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
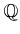
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―Âŋïŋ―āž°ïŋ―ïŋ―
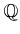
![$ [X,Y]$](img48.png)
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
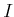
ïŋ―ïŋ―
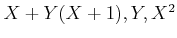
ïŋ―ōļĩĪČĪïŋ―ïŋ―ÆīÞĪïŋ―ïŋ―ïŋ―ïŋ―
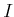
ïŋ―ïŋ―
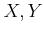
ïŋ―âļĩïŋ―ČĪïŋ―ïŋ―ÆīÞĪāĪģïŋ―ČĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 3.1
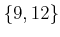
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
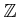
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
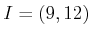
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―
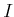 ïŋ―Ï°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
ïŋ―Ï°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―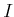 ïŋ―ïŋ―
ïŋ―ïŋ―
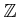 ïŋ―ËĪïŋ―ïŋ―ÝĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
ïŋ―ËĪïŋ―ïŋ―ÝĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
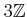 ïŋ―ïŋ―
ïŋ―ïŋ― 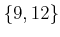 ïŋ―ïŋ―ÞĪïŋ―
ïŋ―ïŋ―ÞĪïŋ―
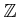 ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒ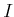 ïŋ―ΚĮūïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ęĄĒ
ïŋ―ΚĮūïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ęĄĒ
ïŋ―Ęūïŋ―ËĪïŋ―ęĄĒ
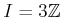 ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―(
ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―(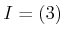 ïŋ―Č―ņĪĪĪÆĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―âŧēïŋ―ïŋ―)
ïŋ―Č―ņĪĪĪÆĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―âŧēïŋ―ïŋ―)



Next: About this document ...
2014-12-19
![]()
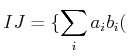 Íïŋ―ïŋ―ïŋ―ïŋ―
Íïŋ―ïŋ―ïŋ―ïŋ―