


Next: About this document ...
Resolutions of singularities.
Yoshifumi Tsuchimoto
PROPOSITION 05.1
For any ring 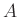 , the map
, the map
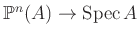 is proper.
is proper.
PROOF..
See http://amathew.wordpress.com/2010/10/23/a-projective-morphism-is-proper/.
COROLLARY 05.2
For any ring 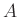 and for any
and for any
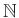 -graded ring
-graded ring
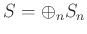 which is generated by a finite subset of
which is generated by a finite subset of 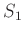 over the ring
over the ring
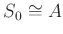 , the map
, the map
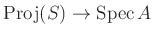 is proper.
is proper.
DEFINITION 05.4
Let
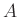
be a commutative ring. Let
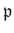
be its prime ideal. Then we define
the localization of
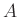
with respect to
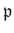
by
DEFINITION 05.5
A commutative ring
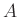
is said to be a local ring if it has only one
maximal ideal.
LEMMA 05.7
- Let
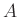 be a local ring. Then the maximal ideal of
be a local ring. Then the maximal ideal of 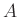 coincides with
coincides with
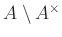 .
.
- A commutative ring
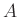 is a local ring if and only if
the set
is a local ring if and only if
the set
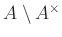 of non-units of
of non-units of 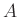 forms an ideal of
forms an ideal of 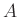 .
.
PROOF..
(1) Assume
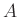
is a local ring with the maximal ideal
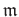
.
Then for any element
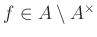
,
an ideal
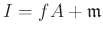
is an ideal of
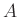
.
By Zorn's lemma, we know that
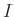
is contained in a maximal ideal of
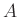
.
From the assumption, the maximal ideal should be
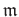
.
Therefore, we have
which shows that
The converse inclusion being obvious (why?), we have
(2) The ``only if'' part is an easy corollary of (1).
The ``if'' part is also easy.
COROLLARY 05.8
Let 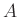 be a commutative ring. Let
be a commutative ring. Let
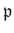 its prime ideal. Then
its prime ideal. Then
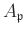 is
a local ring with the only maximal ideal
is
a local ring with the only maximal ideal
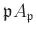 .
.
DEFINITION 05.9
Let
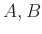
be local rings
with maximal ideals
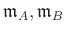
respectively.
A local homomorphism
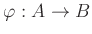
is a homomorphism which
preserves maximal ideals. That means, a homomorphism
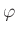
is said to be loc
al
if
EXAMPLE 05.10 (of NOT being a local homomorphism)
is not a local homomorphism.
PROPOSITION 05.12
Let 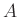 be a commutative ring. let
be a commutative ring. let 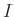 be an ideal of
be an ideal of 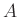 such that
such that
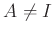 . Then there exists a maximal ideal
. Then there exists a maximal ideal
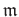 of
of 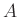 which contains
which contains 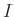 .
.
PROOF..
Since
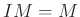
, there exists elements
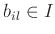
such that
holds. In a matrix notation, this may be rewritten as
with
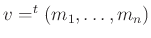
,
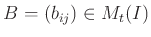
.
Using the unit matrix
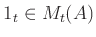
one may also write :
Now let
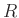
be the adjugate matrix of
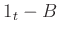
. In other words, it
is a matrix which satisfies
Then we have
On the other hand, since
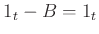
modulo
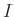
, we have
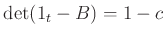
for some
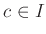
. This
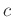
clearly satisfies
We need a criterion for regularity. Instead of developing the
vast theory of regular rings, we site here the following theorem:



Next: About this document ...
2014-05-30
![]() be an ideal of a ring
be an ideal of a ring ![]() generated by elements
generated by elements
![]() .
Assume that each of the elements
.
Assume that each of the elements
![]() is not a zero divisor
in
is not a zero divisor
in ![]() . Then:
. Then:
![]()
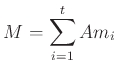
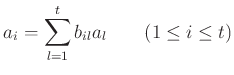
![]()