пњљпњљ 2пњљпњљпњљ№§ќЉпњљпњљпњљ :
![]()
пњљпњљ
![]() пњљпњљ
пњљѕ°пњљпњљ÷§…§пњљпњљ
пњљпњљ
пњљѕ°пњљпњљ÷§…§пњљпњљ ![]() пњљпњљпњљ–§пњљпњљ∆§в°Ґ
пњљпњљпњљ–§пњљпњљ∆§в°Ґ ![]() пњљпњљпњљ §к§њпњљƒ°„§»§пњљпњљпњљпњљпњљћ£пњљпњљ
пњљпњљпњљ §к§њпњљƒ°„§»§пњљпњљпњљпњљпњљћ£пњљпњљ
пњљпњљ
![]() пњљпњљ
пњљѕ°пњљпњљ÷§ §Ћ§пњљпњљпњљпњљпњљпњљƒ§пњљ
пњљпњљ
пњљѕ°пњљпњљ÷§ §Ћ§пњљпњљпњљпњљпњљпњљƒ§пњљ ![]() пњљпњљпњљ–§пњљпњљ∆§ѕ°пњљ
пњљпњљпњљ–§пњљпњљ∆§ѕ°пњљ ![]() пњљпњљпњљ §к§њпњљƒ°„§»§пњљпњљпњљпњљпњљћ£пњљпњљпњљ—§пњљпњљл°£
пњљпњљпњљ §к§њпњљƒ°„§»§пњљпњљпњљпњљпњљћ£пњљпњљпњљ—§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ§ќ§пњљпњљ»§т§≥§ќє÷µпњљпњљ«§пњљ
![]() пњљ»љс§ѓ°пњљ
пњљпњљпњљпњљ»§ѕ°пњљпњљпњљпњљпњљ≈™пњљЋ§ѕЉпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљ»љс§ѓ°пњљ
пњљпњљпњљпњљ»§ѕ°пњљпњљпњљпњљпњљ≈™пњљЋ§ѕЉпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљ §к§њпњљƒ§»§пњљпњљЋЄпњљпњљпњљпњљпњљ
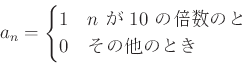
пњљпњљпњљпњљпњљпњљпњљпњљпњљ»§пњљпњљпњљ
(пњљпњљпњљпњљ) пњљпњљпњљпњљЋ°пњљ«°пњљ![]() пњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљ ![]() пњљЋЉпњљ¬Ђпњљпњљпњљпњљпњљ»§пњљпњљл°£
пњљпњљ¬Ђпњљпњљпњљпњљпњљпњљпњљ
пњљЋЉпњљ¬Ђпњљпњљпњљпњљпњљ»§пњљпњљл°£
пњљпњљ¬Ђпњљпњљпњљпњљпњљпњљпњљ ![]() пњљ»§пњљпњљпњљ
пњљ»§пњљпњљпњљ
![]() пњљпњљпњљпњљ—§пњљпњљи§¶пњљпњљ
пњљпњљпњљпњљ
пњљпњљпњљпњљ—§пњљпњљи§¶пњљпњљ
пњљпњљпњљпњљ ![]() пњљпњљ¬Єпњљя§пњљпњљ∆°пњљ
пњљпњљ¬Єпњљя§пњљпњљ∆°пњљ
| (пњљпњљ) | 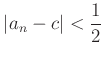 |
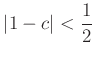
пњљпњљпњљп§Ђпњљк°Ґ
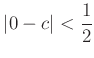
пњљпњљпњљп§Ђпњљл°£
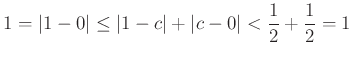
пњљ»§ §√§пњљћЈпњљпњљ«§пњљпњљл°£
пњљпњљ√§∆°пњљ![]() пњљѕ§пњљпњљпњљпњљ §пњљпњљЌ§Ћ§пњљпњљ¬Ђпњљпњљпњљ §пњљпњљпњљ
пњљѕ§пњљпњљпњљпњљ §пњљпњљЌ§Ћ§пњљпњљ¬Ђпњљпњљпњљ §пњљпњљпњљ
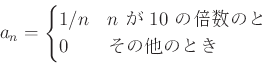
пњљпњљпњљпњљпњљпњљпњљпњљпњљ»§пњљпњљпњљ
(пњљпњљпњљпњљ)
Ќњпњљпњљпњљпњљм§њ
![]()
![]()
![]() пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
![]() пњљ»§пњљпњљ∆°пњљ
пњљ»§пњљпњљ∆°пњљ
![]() пњљпњљпњљпњљз§≠пњљпњљпњљпњљпњљпњљпњљпњљпњљƒ§»§√§∆§пњљпњљпњљпњљпњљ
(пњљпњљпњљќ§и§¶пњљ §пњљпњљ(пњљпњљпњљ §пњљпњљЌњпњљпњљпњљпњљм§њпњљ¬њпњљпњљпњљпњљпњљпњљз§≠пњљпњљпњљпњљпњљпњљ)
пњљпњљ¬Єпњљя§пњљпњљл§≥пњљ»§ѕ°пњљпњљ÷•пњљпњљл•≠пњљпњљ«•пњљпњљќЄпњљпњљпњљпњљ„§»§пњљпњљпњљ
пњљЁЊЏ§пњљпњљпњљ∆§пњљпњљл§ђпњљпњљпњљё•пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ√§∆§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ»ї„§√§∆§пњљпњљ…§пњљпњљпњљ)
пњљпњљпњљпњљз§≠пњљпњљпњљпњљпњљпњљпњљпњљпњљƒ§»§√§∆§пњљпњљпњљпњљпњљ
(пњљпњљпњљќ§и§¶пњљ §пњљпњљ(пњљпњљпњљ §пњљпњљЌњпњљпњљпњљпњљм§њпњљ¬њпњљпњљпњљпњљпњљпњљз§≠пњљпњљпњљпњљпњљпњљ)
пњљпњљ¬Єпњљя§пњљпњљл§≥пњљ»§ѕ°пњљпњљ÷•пњљпњљл•≠пњљпњљ«•пњљпњљќЄпњљпњљпњљпњљ„§»§пњљпњљпњљ
пњљЁЊЏ§пњљпњљпњљ∆§пњљпњљл§ђпњљпњљпњљё•пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ√§∆§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ»ї„§√§∆§пњљпњљ…§пњљпњљпњљ)
пњљпњљпњљпњљ ![]() пњљпњљпњљпњљ¬Ђпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљ¬Ђпњљпњљпњљпњљпњљпњљпњљ ![]() пњљпњљпњљпњљпњљпњљћ§пњљпњљпњљпњљпњљпњљ»§тЉ®§пњљпњљпњљпњљпњљ
пњљ¬ЇЁ°пњљ
пњљпњљпњљпњљпњљпњљћ§пњљпњљпњљпњљпњљпњљ»§тЉ®§пњљпњљпњљпњљпњљ
пњљ¬ЇЁ°пњљ ![]() пњљ §пњљ«§пњљ’§пњљ
пњљ §пњљ«§пњљ’§пњљ ![]() пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
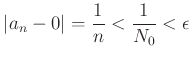
пњљ»§ §√§∆°пњљпњљпњљпњљпњљпњљпњљќЊпњљпњљЋ§пњљпњљпњљ
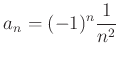
пњљпњљпњљпњљпњљпњљпњљпњљпњљ»§пњљпњљпњљ
«∞пњљќ§пњљпњљб•Ґпњљл•≠пњљпњљ«•пњљпњљќЄпњљпњљпњљпњљќ•пњљпњљ∆°пњљпњљ»•пњљпњљ»§пњљ“§ў§∆§пњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ§пњљ¬Єпњљя§пњљпњљл°£
пњљпњљпњљќ§пњљ ![]() пњљ«≥пњљ√§∆§пњљпњљпњљпњљ–°пњљпњљпњљпњљќ§и§¶пњљЋЄпњљпњљпњљпњљпњљпњљпњљпњљ∆§пњљи§§:
пњљ…§ќ§и§¶пњљ Љ¬њпњљпњљпњљпњљ–§пњљпњљ∆§в°Ґпњљпњљпњљпњљпњљпњљпњљпњљз§≠пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
¬Єпњљя§пњљпњљл°£
пњљ«≥пњљ√§∆§пњљпњљпњљпњљ–°пњљпњљпњљпњљќ§и§¶пњљЋЄпњљпњљпњљпњљпњљпњљпњљпњљ∆§пњљи§§:
пњљ…§ќ§и§¶пњљ Љ¬њпњљпњљпњљпњљ–§пњљпњљ∆§в°Ґпњљпњљпњљпњљпњљпњљпњљпњљз§≠пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
¬Єпњљя§пњљпњљл°£