


Next: About this document ...
пњљпњљпњљпњљпњљIIIпњљпњљпњљпњљ No.11
пњљпњљпњљпњљ
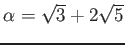 ,
,
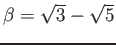 пњљ»§пњљпњљпњљпњљ»§пњљпњљпњљ
пњљ»§пњљпњљпњљпњљ»§пњљпњљпњљ
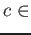
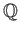 ,
,
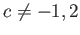 пњљ §пњљпњљ
пњљ §пњљпњљ
[пњљпњљпњљпњљ]
пњљпњљпњљќ•пњљпњљ∆•√•„§«Њпњљпњљпњљпњљпњљпњљл°£
-
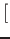
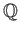
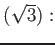
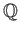
![$ ]=2. $](img11.png)
-
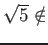
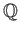

-
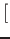
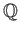
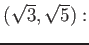
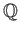
![% latex2html id marker 976
$ (\sqrt{3})]=2$](img15.png) .
.
-
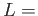
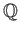
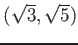 пњљпњљ
пњљпњљ
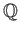 пњљќ•пњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљ√§∆°пњљ
пњљпњљпњљќ≥пњљпњљзЉ°пњљпњљпњљпњљ
пњљќ•пњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљ√§∆°пњљ
пњљпњљпњљќ≥пњљпњљзЉ°пњљпњљпњљпњљ 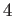 .
.
-

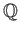
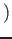 пњљќЄпњљ
пњљќЄпњљ 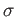 пњљпњљ
пњљпњљ 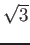 пњљќє‘§пњљпњљпњљ
пњљќє‘§пњљпњљпњљ
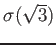 (
(
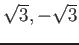 пњљпњљпњљпњљпњљћ§к°£)
пњљпњљ
пњљпњљпњљпњљпњљћ§к°£)
пњљпњљ 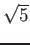 пњљќє‘§пњљпњљпњљ
пњљќє‘§пњљпњљпњљ
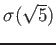 (
(
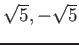 пњљпњљпњљпњљпњљћ§пњљ)
пњљЋ§пњљпњљпњљпњљё§л°£пњљпњљпњљпњљпњљв°Ґпњљпњљпњљпњљпњљ (
пњљпњљпњљпњљпњљћ§пњљ)
пњљЋ§пњљпњљпњљпњљё§л°£пњљпњљпњљпњљпњљв°Ґпњљпњљпњљпњљпњљ (
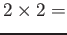 ) 4пњљћ§пњљпњљпњљ»§яєпњљп§їпњљпњљ
пњљпњљпњљў§∆•пњљпњљпњљпњљпњљпњљпњљпњљќЄпњљ
пњљ»§пњљпњљ∆Єпњљпњљпњљл°£
) 4пњљћ§пњљпњљпњљ»§яєпњљп§їпњљпњљ
пњљпњљпњљў§∆•пњљпњљпњљпњљпњљпњљпњљпњљќЄпњљ
пњљ»§пњљпњљ∆Єпњљпњљпњљл°£
-
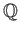
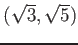 пњљпњљ
пњљпњљ
 пњљў•пњљпњљ»•пњљпњљпњљ÷§»§пњљпњљ∆§ќіпњљпњљпњљ»§пњљпњљпњљ
пњљў•пњљпњљ»•пњљпњљпњљ÷§»§пњљпњљ∆§ќіпњљпњљпњљ»§пњљпњљпњљ
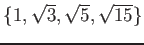 пњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
-
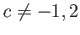 пњљ §й°Ґ пњљпњљпњљпњљпњљпњљпњљпњљ
пњљ §й°Ґ пњљпњљпњљпњљпњљпњљпњљпњљ

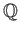
 пњљќЄпњљпњљ«°пњљ
пњљќЄпњљпњљ«°пњљ
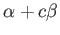 пњљпњљ∆∞пњљпњљпњљпњљпњљ §пњљпњљпњљќ§ѕ°пњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ√±пњљћЄпњљ(пњљпњљпњљпњљпњљпњљпњљпњљ)пњљЋЄ¬§л°£
пњљпњљ∆∞пњљпњљпњљпњљпњљ §пњљпњљпњљќ§ѕ°пњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ√±пњљћЄпњљ(пњљпњљпњљпњљпњљпњљпњљпњљ)пњљЋЄ¬§л°£
пњљпњљќ§и§¶пњљЋ°пњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ§√§пњљпњљпњљ«§ §й°Ґпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ∆§пњљ ђпњљпњљпњљпњљд§єпњљпњљпњљ §л°£
(пњљпњљпњљпњљпњљпњљпњљкЉЂпњљќ§ѕ°пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќєпњљпњљџ§пњљпњљќ§пњљќ§пњљ…ђпњљ„§«§пњљпњљ√§пњљпњљќ§«°пњљ
пњљпњљпњљпњљпњљпњљпњљќіпњљпњљпњљпњљпњљпњљпњљ(пњљпњљпњљпњљпњљпњљпњљ–±пњљ)пњљпњљпњљ—§пњљпњљпњљпњљЋЊпњљпњљпњљпњљпњљпњљпњљ…ђпњљ„§пњљпњљпњљпњљ√§пњљпњљпњљ)
пњљпњљпњљпњљ 11.1 (пњљпњљпњљпњљ6.8пњљ∆Јпњљ)
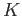
пњљпњљћµпњљ¬Єƒ§ќЄпњљпњљпњљпњљпњљпњљпњљќ§»§пњљпњљл°£
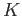
пњљпњљпњљпњљпњљпњљ≈™пњљ Єпњљ
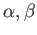
пњљпњљпњљпњљпњљ»§пњљпњљ
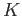
пњљпњљ ђќ•≈™пњљ §пњљпњљ
пњљпњљя§пњљпњљпњљ
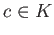
пњљпњљпњљпњљпњљ §пњљпњљ»§пњљ“§»§пњљ¬Єпњљя§пњљпњљл°£
пњљпњљ≈ЇпњљпњљпњљЋ§ƒ§пњљпњљ∆°пњљ
пњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљл°£
пњљƒ§ё§к°Ґ
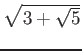 пњљѕ°пњљпњљпњљпњљ’§ќ§и§¶пњљЋіпњљ√±пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљ≈Їпњљпњљпњљпњљѕ§пњљпњљпњљпњљ»§пњљпњљпњљпњљпњљ
∆±пњљЌ§Ћ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ©пњљƒ§пњљпњљ»§пњљпњљп§Ђпњљл°£
пњљѕ°пњљпњљпњљпњљ’§ќ§и§¶пњљЋіпњљ√±пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљ≈Їпњљпњљпњљпњљѕ§пњљпњљпњљпњљ»§пњљпњљпњљпњљпњљ
∆±пњљЌ§Ћ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ©пњљƒ§пњљпњљ»§пњљпњљп§Ђпњљл°£
пњљпњљпњљпњљпњљ«°пњљ
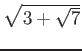 пњљѕЊпњљќ§и§¶пњљЋ§ѕіпњљ√±пњљЋ§ §пњљ §пњљпњљпњљ
пњљпњљпњљпњљѕ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљѕЊпњљќ§и§¶пњљЋ§ѕіпњљ√±пњљЋ§ §пњљ §пњљпњљпњљ
пњљпњљпњљпњљѕ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
-
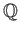 пњљќ•пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљќ•пњљпњљпњљпњљпњљпњљпњљпњљпњљ 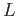 пњљ«°пњљ
пњљ«°пњљ
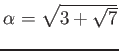 пњљпњљ
пњљпњљпњљ»§пњљпњљ∆іё§пњљпњљќ§ѕ°пњљ
пњљпњљ
пњљпњљпњљ»§пњљпњљ∆іё§пњљпњљќ§ѕ°пњљ
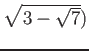 пњљвЄµпњљ»§пњљпњљ∆іё§а°£
пњљвЄµпњљ»§пњљпњљ∆іё§а°£
-
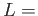
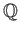
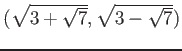 .
.
-
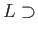
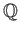
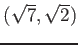 .
.
-
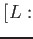
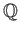
![% latex2html id marker 1064
$ (\sqrt{7},\sqrt{2})]=2$](img48.png) .
.
- пњљв§Јпњљпњљ
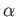 пњљпњљЌ≠пњљпњљпњљпњљ
пњљпњљЌ≠пњљпњљпњљпњљ 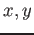 пњљ«§пњљ√§пњљ
пњљ«§пњљ√§пњљ
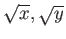 пњљпњљЌ≠пњљпњљпњљпњљпњљпњљпњљпњљЌ≠пњљпњљпњљпњљпњљ»§пњљпњљ∆§пњљпњљпњљпњљпњљ §й°Ґ
пњљпњљЌ≠пњљпњљпњљпњљпњљпњљпњљпњљЌ≠пњљпњљпњљпњљпњљ»§пњљпњљ∆§пњљпњљпњљпњљпњљ §й°Ґ
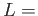
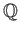
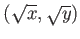 пњљпњљ
пњљ §√§∆°пњљпњљпњљќїпњљпњљ¬§пњљћЈпњљв§єпњљл°£
пњљпњљ
пњљ §√§∆°пњљпњљпњљќїпњљпњљ¬§пњљћЈпњљв§єпњљл°£
2014-01-16
![]() ,
,
![]() пњљ»§пњљпњљпњљпњљ»§пњљпњљпњљ
пњљ»§пњљпњљпњљпњљ»§пњљпњљпњљ
![]()
![]() ,
,
![]() пњљ §пњљпњљ
пњљ §пњљпњљ
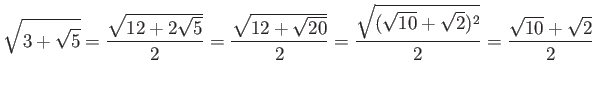
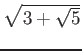 пњљѕ°пњљпњљпњљпњљ’§ќ§и§¶пњљЋіпњљ√±пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљ≈Їпњљпњљпњљпњљѕ§пњљпњљпњљпњљ»§пњљпњљпњљпњљпњљ
∆±пњљЌ§Ћ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ©пњљƒ§пњљпњљ»§пњљпњљп§Ђпњљл°£
пњљѕ°пњљпњљпњљпњљ’§ќ§и§¶пњљЋіпњљ√±пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљ≈Їпњљпњљпњљпњљѕ§пњљпњљпњљпњљ»§пњљпњљпњљпњљпњљ
∆±пњљЌ§Ћ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ©пњљƒ§пњљпњљ»§пњљпњљп§Ђпњљл°£
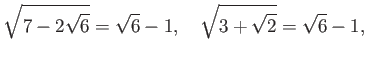
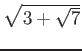 пњљѕЊпњљќ§и§¶пњљЋ§ѕіпњљ√±пњљЋ§ §пњљ §пњљпњљпњљ
пњљпњљпњљпњљѕ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљѕЊпњљќ§и§¶пњљЋ§ѕіпњљ√±пњљЋ§ §пњљ §пњљпњљпњљ
пњљпњљпњљпњљѕ°пњљпњљпњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
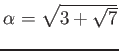 пњљпњљ
пњљпњљпњљ»§пњљпњљ∆іё§пњљпњљќ§ѕ°пњљ
пњљпњљ
пњљпњљпњљ»§пњљпњљ∆іё§пњљпњљќ§ѕ°пњљ
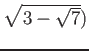 пњљвЄµпњљ»§пњљпњљ∆іё§а°£
пњљвЄµпњљ»§пњљпњљ∆іё§а°£
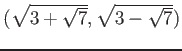 .
.