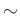 ��Ʊ�ʹط��Ǥ��뤳�Ȥ��ʤ�����
��Ʊ�ʹط��Ǥ��뤳�Ȥ��ʤ�����
- �ʲ���������Ǥϡ�
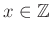 ��
�� 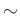 �˴ؤ��륯�饹��
�˴ؤ��륯�饹�� ![$ [x]$](img5.png) �Ƚ�
�Ƚ�
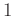 �Υ��饹
�Υ��饹 ![$ [1]$](img7.png) ��°����
��°����
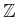 �θ��٤������ʤ�����
�θ��٤������ʤ�����
-
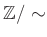 ����
����
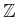 �ؤμ���
�ؤμ���  ��
��
![$ f([x])=$](img10.png) ($x$ �� $3$ �dz�ä�;��)
������Ǥ������������
($x$ �� $3$ �dz�ä�;��)
������Ǥ������������
-
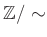 ����
����
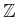 �ؤμ���
�ؤμ���  ��
��
![$ f([x])=$](img10.png) ($x$ �� $4$ �dz�ä�;��)
������Ǥ������������
($x$ �� $4$ �dz�ä�;��)
������Ǥ������������